
ЁОЬтФПЁПФГЪГЦЗЕФБЃЯЪЪБМфtЃЈЕЅЮЛЃКаЁЪБЃЉгыДЂВиЮТЖШxЃЈЕЅЮЛЃКЁцЃЉТњзуКЏЪ§ЙиЯЕt=![]() ЧвИУЪГЦЗдк4ЁцЕФБЃЯЪЪБМфЪЧ16аЁЪБЁЃвбжЊМздкФГШеЩЯЮч10ЪБЙКТђСЫИУЪГЦЗЃЌВЂНЋЦфвХЗХдкЪвЭтЃЌЧвДЫШеЕФЪвЭтЮТЖШЫцЪБМфБфЛЏШчЭМЫљЪОЁЃИјГівдЯТЫФИіНсТлЃК
ЧвИУЪГЦЗдк4ЁцЕФБЃЯЪЪБМфЪЧ16аЁЪБЁЃвбжЊМздкФГШеЩЯЮч10ЪБЙКТђСЫИУЪГЦЗЃЌВЂНЋЦфвХЗХдкЪвЭтЃЌЧвДЫШеЕФЪвЭтЮТЖШЫцЪБМфБфЛЏШчЭМЫљЪОЁЃИјГівдЯТЫФИіНсТлЃК
ЂйИУЪГЦЗдк6ЁцЕФБЃЯЪЪБМфЪЧ8аЁЪБЃЛ
ЂкЕБxЁЪ[-6ЃЌ6]ЪБЃЌИУЪГЦЗЕФБЃЯЪЪБМфtЫцзХxдіДѓЖјж№НЅМѕЩйЃЛ
ЂлЕНСЫДЫШе13ЪБЃЌМзЫљЙКТђЕФЪГЦЗЛЙдкБЃЯЪЪБМфФкЃЛ
ЂмЕНСЫДЫШе14ЪБЃЌМзЫљЙКТђЕФЪГЦЗвбШЛЙ§СЫБЃЯЪЪБМфЁЃ
ЦфжаЃЌЫљгае§ШЗНсТлЕФађКХЪЧ__________ЁЃ
ЁОД№АИЁПЂйЂм
ЁОНтЮіЁПЁпЪГЦЗЕФБЃЯЪЪБМф![]() ЃЈЕЅЮЛЃКаЁЪБЃЉгыДЂВиЮТЖШ
ЃЈЕЅЮЛЃКаЁЪБЃЉгыДЂВиЮТЖШ![]() ЃЈЕЅЮЛЃКЁцЃЉТњзуКЏЪ§ЙиЯЕ
ЃЈЕЅЮЛЃКЁцЃЉТњзуКЏЪ§ЙиЯЕ![]() ЧвИУЪГЦЗдк4ЁцЕФБЃЯЪЪБМфЪЧ
ЧвИУЪГЦЗдк4ЁцЕФБЃЯЪЪБМфЪЧ![]() аЁЪБЃЌЁр
аЁЪБЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЁр
ЃЌЁр ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЙЪЂйИУЪГЦЗдк6ЁцЕФБЃЯЪЪБМфЪЧ8аЁЪБЃЌе§ШЗЃЛЂкЕБ
ЃЌЙЪЂйИУЪГЦЗдк6ЁцЕФБЃЯЪЪБМфЪЧ8аЁЪБЃЌе§ШЗЃЛЂкЕБ![]() ЪБЃЌБЃЯЪЪБМфКуЮЊ64аЁЪБЃЌЕБ
ЪБЃЌБЃЯЪЪБМфКуЮЊ64аЁЪБЃЌЕБ![]() ЪБЃЌИУЪГЦЗЕФБЃЯЪЪБМф
ЪБЃЌИУЪГЦЗЕФБЃЯЪЪБМф![]() ЫцПД
ЫцПД![]() діДѓЖјж№НЅМѕЩйЃЌЙЪДэЮѓЃЛЂлЕНСЫДЫШе10ЪБЃЌЮТЖШГЌЙ§8ЖШЃЌДЫЪББЃЯЪЪБМфВЛГЌЙ§4аЁЪБЃЌЙЪЕН13ЪБЃЌМзЫљЙКТђЕФЪГЦЗВЛдкБЃЯЪЪБМфФкЃЌЙЪДэЮѓЃЛЂмЕНСЫДЫШе14ЪБЃЌМзЫљЙКТђЕФЪГЦЗвбШЛЙ§СЫБЃЯЪЪБМфЃЌЙЪе§ШЗЃЌЙЪе§ШЗЕФНсТлЕФађКХЮЊЂйЂмЃЌЙЪД№АИЮЊЂйЂм.
діДѓЖјж№НЅМѕЩйЃЌЙЪДэЮѓЃЛЂлЕНСЫДЫШе10ЪБЃЌЮТЖШГЌЙ§8ЖШЃЌДЫЪББЃЯЪЪБМфВЛГЌЙ§4аЁЪБЃЌЙЪЕН13ЪБЃЌМзЫљЙКТђЕФЪГЦЗВЛдкБЃЯЪЪБМфФкЃЌЙЪДэЮѓЃЛЂмЕНСЫДЫШе14ЪБЃЌМзЫљЙКТђЕФЪГЦЗвбШЛЙ§СЫБЃЯЪЪБМфЃЌЙЪе§ШЗЃЌЙЪе§ШЗЕФНсТлЕФађКХЮЊЂйЂмЃЌЙЪД№АИЮЊЂйЂм.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(2017ЁЄББОЉИпПМ)гЩЫФРтжљABCDA1B1C1D1НиШЅШ§РтзЖC1B1CD1КѓЕУЕНЕФМИКЮЬхШчЭМЫљЪОЃЎЫФБпаЮABCDЮЊе§ЗНаЮЃЌOЮЊACгыBDЕФНЛЕуЃЌEЮЊADЕФжаЕуЃЌA1EЁЭЦНУцABCD.

(1)жЄУїЃКA1OЁЮЦНУцB1CD1ЃЛ
(2)ЩшMЪЧODЕФжаЕуЃЌжЄУїЃКЦНУцA1EMЁЭЦНУцB1CD1.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖPЃABCDжаЃЌPAЁЭЕзУцABCDЃЌADЁЮBCЃЌABЃНADЃНACЃН3ЃЌPAЃНBCЃН4ЃЌMЮЊЯпЖЮADЩЯвЛЕуЃЌAMЃН2MDЃЌNЮЊPCЕФжаЕуЃЎ

(1)жЄУїMNЁЮЦНУцPABЃЛ
(2)ЧѓЫФУцЬхNЃBCMЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖSЉABCDжаЃЌABЁЮCDЃЌBCЁЭCDЃЌВрУцSABЮЊЕШБпШ§НЧаЮЃЎAB=BC=2ЃЌCD=SD=1ЃЎ 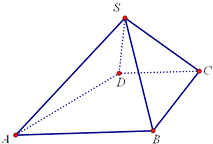
ЃЈ1ЃЉжЄУїЃКSDЁЭЦНУцSAB
ЃЈ2ЃЉЧѓABгыЦНУцSBCЫљГЩНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§![]() ЃЌІиЃО0ЃЌ|Іе|ЃМ
ЃЌІиЃО0ЃЌ|Іе|ЃМ![]() ЃЉЕФвЛИіСуЕугыжЎЯрСкЕФЖдГЦжсжЎМфЕФОрРыЮЊ
ЃЉЕФвЛИіСуЕугыжЎЯрСкЕФЖдГЦжсжЎМфЕФОрРыЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЪБfЃЈxЃЉгазюаЁжЕЃЎ
ЪБfЃЈxЃЉгазюаЁжЕЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓfЃЈxЃЉЕФжЕгђЃЎ
ЃЌЧѓfЃЈxЃЉЕФжЕгђЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§gЃЈxЃЉ=ax2-2ax+1+bЃЈa>0ЃЉдкЧјМф[2ЃЌ4]ЩЯЕФзюДѓжЕЮЊ9ЃЌзюаЁжЕЮЊ1ЃЌМЧfЃЈxЃЉ=gЃЈ|x|ЃЉЁЃ
ЃЈ1ЃЉЧѓЪЕЪ§aЃЌbЕФжЕЃЛ
ЃЈ2ЃЉШєВЛЕШЪНfЃЈ2kЃЉ>1ГЩСЂЃЌЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЖЈвхдк[pЃЌq]ЩЯЕФКЏЪ§![]() ЃЈxЃЉЃЌЩшp=x0<x1<Ё<xi-1<xi<Ё<xn=qЃЌx1ЃЌx2ЃЌЁЃЌxn-lНЋЧјМф[pЃЌq]ШЮвтЛЎЗжГЩnИіаЁЧјМфЃЌШчЙћДцдквЛИіГЃЪ§M>0ЃЌЪЙЕУКЭЪН
ЃЈxЃЉЃЌЩшp=x0<x1<Ё<xi-1<xi<Ё<xn=qЃЌx1ЃЌx2ЃЌЁЃЌxn-lНЋЧјМф[pЃЌq]ШЮвтЛЎЗжГЩnИіаЁЧјМфЃЌШчЙћДцдквЛИіГЃЪ§M>0ЃЌЪЙЕУКЭЪН![]() КуГЩСЂЃЌдђГЦКЏЪ§
КуГЩСЂЃЌдђГЦКЏЪ§![]() ЃЈxЃЉЮЊдк[pЃЌq]ЩЯЕФгаНчБфВюКЏЪ§ЁЃЪдХаЖЯКЏЪ§fЃЈxЃЉЪЧЗёЮЊдк[0ЃЌ4]ЩЯЕФгаНчБфВюКЏЪ§?ШєЪЧЃЌЧѓMЕФзюаЁжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЁЃ
ЃЈxЃЉЮЊдк[pЃЌq]ЩЯЕФгаНчБфВюКЏЪ§ЁЃЪдХаЖЯКЏЪ§fЃЈxЃЉЪЧЗёЮЊдк[0ЃЌ4]ЩЯЕФгаНчБфВюКЏЪ§?ШєЪЧЃЌЧѓMЕФзюаЁжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЃЈ![]() ЃЉЧѓЫФРтзЖ
ЃЉЧѓЫФРтзЖ![]() ЕФЬхЛ§ЃЎ
ЕФЬхЛ§ЃЎ
ЃЈ![]() ЃЉЧѓжЄЃКЦНУц
ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉдкЯпЖЮ
ЃЉдкЯпЖЮ![]() ЩЯШЗЖЈвЛЕу
ЩЯШЗЖЈвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЦНУц
ЦНУц![]() ЃЌВЂИјГіжЄУїЃЎ
ЃЌВЂИјГіжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕxOy жаЃЌвбжЊдВCЕФВЮЪ§ЗНГЬЮЊ ![]() ЃЈІеЮЊВЮЪ§ЃЉЃЎвдзјБъдЕуЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈІеЮЊВЮЪ§ЃЉЃЎвдзјБъдЕуЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈ1ЃЉЧѓдВЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉжБЯпlЕФМЋзјЗНГЬЪЧ ![]() ЃЌЩфЯпOMЃКІШ=
ЃЌЩфЯпOMЃКІШ= ![]() гыдВЕФНЛЕуЮЊOЃЌPЃЌгыжБЯпlЕФНЛЕуЮЊQЃЌЧѓЯпЖЮPQЕФГЄЃЎ
гыдВЕФНЛЕуЮЊOЃЌPЃЌгыжБЯпlЕФНЛЕуЮЊQЃЌЧѓЯпЖЮPQЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцЛњБфСПІЮЕФЗжВМСаШчБэЃЌЦфжаaЃЌbЃЌcГЩЕШВюЪ§СаЃЎШєEЃЈІЮЃЉ= ![]() ЃЌдђDЃЈІЮЃЉ=ЃЈ ЃЉ
ЃЌдђDЃЈІЮЃЉ=ЃЈ ЃЉ
ІЮ | 1 | 2 | 3 |
P | a | b | c |
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com