
【题目】已知点![]() 是椭圆C:
是椭圆C:![]() 上的一点,椭圆C的离心率与双曲线
上的一点,椭圆C的离心率与双曲线![]() 的离心率互为倒数,斜率为
的离心率互为倒数,斜率为![]() 直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
直线l交椭圆C于B,D两点,且A、B、D三点互不重合.

(1)求椭圆C的方程;
(2)若![]() 分别为直线AB,AD的斜率,求证:
分别为直线AB,AD的斜率,求证:![]() 为定值。
为定值。
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
(1)根据椭圆的定义和几何性质,建立方程,即可求椭圆C的方程;
(2)设直线BD的方程为![]() ,代入椭圆方程,设D(x1,y1),B(x2,y2),直线AB、AD的斜率分别为:
,代入椭圆方程,设D(x1,y1),B(x2,y2),直线AB、AD的斜率分别为:![]() ,则
,则 ,由此导出结果.
,由此导出结果.
(1)由题意,可得e=![]() =
=![]() ,代入A(1,
,代入A(1,![]() )得
)得![]() ,
,
又![]() ,解得
,解得![]() ,
,
所以椭圆C的方程![]() .
.
(2)证明:设直线BD的方程为y=![]() x+m,
x+m,

又A、B、D三点不重合,∴![]() ,
,
设D(x1,y1),B(x2,y2),
则由 得4x2+2
得4x2+2![]() mx+m2-4=0
mx+m2-4=0
所以△=-8m2+64>0,所以![]() <m<
<m<![]() .
.
x1+x2=-![]() m,
m,![]()
设直线AB、AD的斜率分别为:kAB、kAD,
则kAD+kAB=
=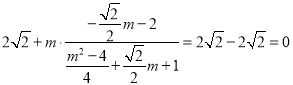
所以kAD+kAB=0,即直线AB,AD的斜率之和为定值.


科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形面积为![]() ,
,![]() ,
,![]() ,
,![]() 为三角形三边长,
为三角形三边长,![]() 为三角形内切圆半径,利用类比推理,可以得出四面体的体积为( )
为三角形内切圆半径,利用类比推理,可以得出四面体的体积为( )
A. ![]()
B. ![]()
C. ![]() (
(![]() 为四面体的高)
为四面体的高)
D. ![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 分别为四面体四个面的面积,
分别为四面体四个面的面积,![]() 为四面体内切球的半径,设四面体的内切球的球心为
为四面体内切球的半径,设四面体的内切球的球心为![]() ,则球心
,则球心![]() 到四个面的距离都是
到四个面的距离都是![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级学生会主席团有共有![]() 名同学组成,其中有
名同学组成,其中有![]() 名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不期而至的新冠肺炎疫情,牵动了亿万国人的心,全国各地纷纷捐赠物资驰援武汉.有一批捐赠物资需要通过轮船沿长江运送至武汉,已知该运送物资的轮船在航行中每小时的燃料费和它的速度的立方成正比,已知当速度为10海里/时时,燃料费是6元/时,而其他与速度无关的费用是96元/时,问当轮船的速度是多少时,航行1海里所需的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]()
![]() ,过抛线
,过抛线![]() 上一点
上一点![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于A、B两点,分别交抛物线于E、F两点,圆心点
相切于A、B两点,分别交抛物线于E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
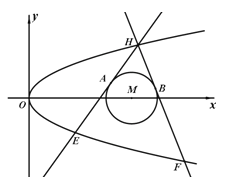
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)当![]() 的角平分线垂直x轴时,求直线EF的斜率;
的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为
,左顶点为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 和
和![]() ,分别交直线
,分别交直线![]() 于
于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄X分别为16岁、18岁、20岁和22岁者,其得肺癌的相对危险度Y依次为15.10,12.81,9.72,3.21;每天吸烟支数U分别为10,20,30者,其得肺癌的相对危险度V分别为7.5,9.5和16.6,用![]() 表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
A.r1=r2B.r1>r2>0
C.0<r1<r2D.r1<0<r2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com