
ĄūĖâÄŋĄŋĄķÉ―ķŦĘĄļßŋžļÄļïĘÔĩã·―°ļĄ·đæķĻĢšīÓ![]() ÄęļßŋžŋŠĘžĢŽļßŋžÎïĀíĄĒŧŊŅ§ĩČÁųÃÅŅĄŋžŋÆÄŋĩÄŋžÉúÔĘžģÉžĻīÓļßĩ―ĩÍŧŪ·ÖΊ
ÄęļßŋžŋŠĘžĢŽļßŋžÎïĀíĄĒŧŊŅ§ĩČÁųÃÅŅĄŋžŋÆÄŋĩÄŋžÉúÔĘžģÉžĻīÓļßĩ―ĩÍŧŪ·ÖΊ![]() °ËļöĩČžķ.ēÎÕÕÕýĖŽ·ÖēžÔÔōĢŽČ·ķĻļũĩČžķČËĘýËųÕžąČĀý·ÖąðΊ
°ËļöĩČžķ.ēÎÕÕÕýĖŽ·ÖēžÔÔōĢŽČ·ķĻļũĩČžķČËĘýËųÕžąČĀý·ÖąðΊ![]() .ŅĄŋžŋÆÄŋģÉžĻžÆČëŋžÉúŨÜģÉžĻĘąĢŽ―Ŧ
.ŅĄŋžŋÆÄŋģÉžĻžÆČëŋžÉúŨÜģÉžĻĘąĢŽ―Ŧ![]() ÖÁ
ÖÁ![]() ĩČžķÄÚĩÄŋžÉúÔĘžģÉžĻĢŽŌĀÕÕĩČąČĀýŨŠŧŧ·ĻÔō·ÖąðŨŠŧŧĩ―
ĩČžķÄÚĩÄŋžÉúÔĘžģÉžĻĢŽŌĀÕÕĩČąČĀýŨŠŧŧ·ĻÔō·ÖąðŨŠŧŧĩ―![]()
![]() °Ëļö·ÖĘýĮøžäĢŽĩÃĩ―ŋžÉúĩÄĩČžķģÉžĻ.
°Ëļö·ÖĘýĮøžäĢŽĩÃĩ―ŋžÉúĩÄĩČžķģÉžĻ.
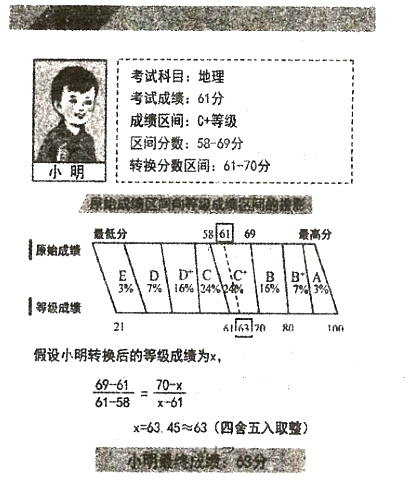
ÄģÐĢ![]() žķŅ§Éúđē
žķŅ§Éúđē![]() ČËĢŽŌÔÆÚÄĐŋžĘÔģÉžĻΊÔĘžģÉžĻŨŠŧŧÁËąūÐĢĩÄĩČžķģÉžĻĢŽÎŠŅ§ÉúšÏĀíŅĄŋÆĖáđĐŌĀūÝĢŽÆäÖÐÎïĀíģÉžĻŧņĩÃĩČžķ
ČËĢŽŌÔÆÚÄĐŋžĘÔģÉžĻΊÔĘžģÉžĻŨŠŧŧÁËąūÐĢĩÄĩČžķģÉžĻĢŽÎŠŅ§ÉúšÏĀíŅĄŋÆĖáđĐŌĀūÝĢŽÆäÖÐÎïĀíģÉžĻŧņĩÃĩČžķ![]() ĩÄŅ§ÉúÔĘžģÉžĻÍģžÆČįÏÂ
ĩÄŅ§ÉúÔĘžģÉžĻÍģžÆČįÏÂ
ģÉžĻ | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
ČËĘý | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
ĢĻ1ĢĐīÓÎïĀíģÉžĻŧņĩÃĩČžķ![]() ĩÄŅ§ÉúÖÐČÎČĄ
ĩÄŅ§ÉúÖÐČÎČĄ![]() ÃûĢŽĮóĮĄšÃÓÐ
ÃûĢŽĮóĮĄšÃÓÐ![]() ÃûÍŽŅ§ĩÄĩČžķ·ÖĘýēŧÐĄÓÚ
ÃûÍŽŅ§ĩÄĩČžķ·ÖĘýēŧÐĄÓÚ![]() ĩÄļÅÂĘ;
ĩÄļÅÂĘ;
ĢĻ2ĢĐīýĩ―ąūžķŅ§Éúļßŋž―áĘøšóĢŽīÓČŦĘĄŋžÉúÖÐēŧ·ÅŧØĩÄËæŧúģéČĄŅ§ÉúĢŽÖąĩ―ģéĩ―![]() ÃûÍŽŅ§ĩÄÎïĀíļßŋžģÉžĻĩČžķΊ
ÃûÍŽŅ§ĩÄÎïĀíļßŋžģÉžĻĩČžķΊ![]() ŧō
ŧō![]() ―áĘø(ŨîķāģéČĄ
―áĘø(ŨîķāģéČĄ![]() ČË)ĢŽÉčģéČĄĩÄŅ§ÉúļöĘýΊ
ČË)ĢŽÉčģéČĄĩÄŅ§ÉúļöĘýΊ![]() ĢŽĮóËæŧúąäÁŋ
ĢŽĮóËæŧúąäÁŋ![]() ĩÄĘýŅ§ÆÚÍû(ŨĒ:
ĩÄĘýŅ§ÆÚÍû(ŨĒ: ![]() ).
).
Ąūīð°ļĄŋ(1)0.29 (2)žû―âÎö
Ąū―âÎöĄŋ
ĢĻ1ĢĐÉčÎïĀíģÉžĻŧņĩÃĩČžķ![]() ĩÄŅ§ÉúÔĘžģÉžĻΊ
ĩÄŅ§ÉúÔĘžģÉžĻΊ![]() ĢŽÆäĩČžķģÉžĻΊ
ĢŽÆäĩČžķģÉžĻΊ![]() ĢŽÓÉÔĘžģÉžĻÓëĩČžķģÉžĻĩÄŨŠŧŧđŦĘ―ĩÃĩ―
ĢŽÓÉÔĘžģÉžĻÓëĩČžķģÉžĻĩÄŨŠŧŧđŦĘ―ĩÃĩ―![]() đØÓÚ
đØÓÚ![]() ĩÄđØÏĩĘ―ĢŽžīŋÉžÆËãģöĩČžķ·ÖĘýēŧÐĄÓÚ
ĩÄđØÏĩĘ―ĢŽžīŋÉžÆËãģöĩČžķ·ÖĘýēŧÐĄÓÚ![]() ĩÄČËĘýĢŽĀûÓÃđÅĩäļÅÐÍžīŋÉžÆËãģöĮĄšÃÓÐ
ĩÄČËĘýĢŽĀûÓÃđÅĩäļÅÐÍžīŋÉžÆËãģöĮĄšÃÓÐ![]() ÃûÍŽŅ§ĩÄĩČžķ·ÖĘýēŧÐĄÓÚ
ÃûÍŽŅ§ĩÄĩČžķ·ÖĘýēŧÐĄÓÚ![]() ĩÄļÅÂĘĄĢ
ĩÄļÅÂĘĄĢ
ĢĻ2ĢĐÓÉĖâŌâĩÃĢŽËæŧúģéČĄ![]() ČËĢŽĩČžķģÉžĻΊ
ČËĢŽĩČžķģÉžĻΊ![]() ŧō
ŧō![]() ĩÄļÅÂĘΊ
ĩÄļÅÂĘΊ![]() ĢŽČŧšóÁÐģöŅ§ÉúļöĘýĩÄ·ÖēžÁÐĢŽžīŋÉžÆËãĘýŅ§ÆÚÍûĄĢ
ĢŽČŧšóÁÐģöŅ§ÉúļöĘýĩÄ·ÖēžÁÐĢŽžīŋÉžÆËãĘýŅ§ÆÚÍûĄĢ
―âĢšĢĻ1ĢĐÉčÎïĀíģÉžĻŧņĩÃĩČžķ![]() ĩÄŅ§ÉúÔĘžģÉžĻΊ
ĩÄŅ§ÉúÔĘžģÉžĻΊ![]() ĢŽÆäĩČžķģÉžĻΊ
ĢŽÆäĩČžķģÉžĻΊ![]() .
.
ÓÉŨŠŧŧđŦĘ―![]() ĢŽĩÃ
ĢŽĩÃ![]() .
.
ÓÉ![]() ĢŽĩÃ
ĢŽĩÃ![]() .
.
ÏÔČŧÔĘžģÉžĻÂúŨã![]() ĩÄÍŽŅ§ÓÐ
ĩÄÍŽŅ§ÓÐ![]() ČËĢŽŧņĩÃĩČžķ
ČËĢŽŧņĩÃĩČžķ![]() ĩÄŅ§ÉúÓÐ
ĩÄŅ§ÉúÓÐ![]() ČËĢŽ
ČËĢŽ
ĮĄšÃÓÐ![]() ÃûÍŽŅ§ĩÄĩČžķ·ÖĘýēŧÐĄÓÚ
ÃûÍŽŅ§ĩÄĩČžķ·ÖĘýēŧÐĄÓÚ![]() ĩÄļÅÂĘΊĢš
ĩÄļÅÂĘΊĢš![]() .
.
ĢĻ2ĢĐÓÉĖâŌâĩÃĢŽËæŧúģéČĄ![]() ČËĢŽÆäĩČžķģÉžĻΊ
ČËĢŽÆäĩČžķģÉžĻΊ![]() ŧō
ŧō![]() ĩÄļÅÂĘΊ
ĩÄļÅÂĘΊ![]() .
.
Ņ§ÉúļöĘý![]() ĩÄŋÉÄÜČĄÖĩΊ
ĩÄŋÉÄÜČĄÖĩΊ![]() Ģŧ
Ģŧ
![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]()
![]() ĢŽ
ĢŽ![]() Ģŧ
Ģŧ
ÆäĘýŅ§ÆÚÍûĘĮĢš
![]()
![]()
![]()
ÆäÖÐĢš
![]() ĒŲ
ĒŲ
![]() ĒÚ
ĒÚ
ÓĶÓÃīíÎŧÏāžõ·ĻĄ°ĒŲĘ―-ĒÚĘ―ĄąĩÃĢš
![]()
![]()
![]()
đĘ![]() .
.


 ÃûĘĶÖļĩžÆÚÄĐģåīĖūíÏĩÁÐīð°ļ
ÃûĘĶÖļĩžÆÚÄĐģåīĖūíÏĩÁÐīð°ļ ŋŠÐÄÍÜŋÚËãĖâŋĻÏĩÁÐīð°ļ
ŋŠÐÄÍÜŋÚËãĖâŋĻÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÍÖÔē![]() ĩÄÓŌ―đĩãΊ
ĩÄÓŌ―đĩãΊ![]() ĢŽÉčÖąÏß
ĢŽÉčÖąÏß![]() Óë
Óë![]() ÖáĩÄ―ŧĩãΊ
ÖáĩÄ―ŧĩãΊ![]() ĢŽđýĩã
ĢŽđýĩã![]() ĮŌÐąÂĘΊ
ĮŌÐąÂĘΊ![]() ĩÄÖąÏß
ĩÄÖąÏß![]() ÓëÍÖÔē―ŧÓÚ
ÓëÍÖÔē―ŧÓÚ![]() Á―ĩãĢŽ
Á―ĩãĢŽ![]() ΊÏßķÎ
ΊÏßķÎ![]() ĩÄÖÐĩã.
ĩÄÖÐĩã.

ĢĻ1ĢĐČôÖąÏß![]() ĩÄĮãÐą―ĮΊ
ĩÄĮãÐą―ĮΊ![]() ĢŽĮó
ĢŽĮó![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ2ĢĐÉčÖąÏß![]() ―ŧÖąÏß
―ŧÖąÏß![]() ÓÚĩã
ÓÚĩã![]() ĢŽÖĪÃũĢšÖąÏß
ĢŽÖĪÃũĢšÖąÏß![]() .
.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÍÖÔē![]() ĩÄĀëÐÄÂĘΊ
ĩÄĀëÐÄÂĘΊ![]() ĢŽđýÍÖÔēĩÄ―đĩãĮŌÓëģĪÖáīđÖąĩÄÏŌģĪΊ1ĢŪ
ĢŽđýÍÖÔēĩÄ―đĩãĮŌÓëģĪÖáīđÖąĩÄÏŌģĪΊ1ĢŪ
ĢĻ1ĢĐĮóÍÖÔēCĩÄ·―ģĖĢŧ
ĢĻ2ĢĐÉčĩãMΊÍÖÔēÉÏĩÚŌŧÏóÏÞÄÚŌŧķŊĩãĢŽAĢŽB·ÖąðΊÍÖÔēĩÄŨóķĨĩãšÍÏÂķĨĩãĢŽÖąÏßMBÓëxÖá―ŧÓÚĩãCĢŽÖąÏßMAÓëyÖá―ŧÓÚĩãDĢŽĮóÖĪĢšËÄąßÐÎABCDĩÄÃæŧýΊķĻÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŧļö°ĩÏäÖÐÓÐÐÎŨīšÍīóÐĄÍęČŦÏāÍŽĩÄ3Öŧ°ŨĮōÓë2ÖŧšÚĮōĢŽÃŋīÎīÓÖÐČĄģöŌŧÖŧĮōĢŽČĄĩ―°ŨĮōĩÃ2·ÖĢŽČĄĩ―šÚĮōĩÃ3·ÖĢŪžŨīÓ°ĩÏäÖÐÓзÅŧØĩØŌĀīÎČĄģö3ÖŧĮōĢŪ
ĢĻ1ĢĐĮóžŨČýīÎķžČĄĩðŨĮōĩÄļÅÂĘĢŧ
ĢĻ2ĢĐĮóžŨŨÜĩ÷ÖĶÎĩÄ·ÖēžÁКÍĘýŅ§ÆÚÍûĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŅĄÐÞ4-4ĢšŨøąęÏĩÓëēÎĘý·―ģĖ
ÔÚÖą―ĮŨøąęÏĩ![]() ÖÐĢŽÖąÏß
ÖÐĢŽÖąÏß![]() ĩÄēÎĘý·―ģĖΊ
ĩÄēÎĘý·―ģĖΊ![]() ĢĻÆäÖÐ
ĢĻÆäÖÐ![]() ΊēÎĘýĢĐ.ÔÚŌÔŨøąęÔĩã
ΊēÎĘýĢĐ.ÔÚŌÔŨøąęÔĩã![]() ΊžŦĩãĢŽŌÔ
ΊžŦĩãĢŽŌÔ![]() ÖáÕý°ëÖáΊžŦÖá―ĻÁĒĩÄžŦŨøąęÏĩÖÐĢŽĮúÏß
ÖáÕý°ëÖáΊžŦÖá―ĻÁĒĩÄžŦŨøąęÏĩÖÐĢŽĮúÏß![]() ĩÄžŦŨøąę·―ģĖΊ
ĩÄžŦŨøąę·―ģĖΊ![]() ĢŽĮúÏß
ĢŽĮúÏß![]() ĩÄÖą―ĮŨøąę·―ģĖΊ
ĩÄÖą―ĮŨøąę·―ģĖΊ![]() .
.
ĢĻ1ĢĐĮóÖąÏß![]() ĩÄžŦŨøąę·―ģĖšÍĮúÏß
ĩÄžŦŨøąę·―ģĖšÍĮúÏß![]() ĩÄÖą―ĮŨøąę·―ģĖĢŧ
ĩÄÖą―ĮŨøąę·―ģĖĢŧ
ĢĻ2ĢĐČôÖąÏß![]() ÓëĮúÏß
ÓëĮúÏß![]() ·ÖąðÏā―ŧÓÚŌėÓÚÔĩãĩÄĩã
·ÖąðÏā―ŧÓÚŌėÓÚÔĩãĩÄĩã![]() ĢŽĮó
ĢŽĮó![]() ĩÄČĄÖĩ·ķΧ.
ĩÄČĄÖĩ·ķΧ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÁ―ģĮĘÐ![]() šÍ
šÍ![]() Ïāūā
Ïāūā![]() ĢŽÏÖžÆŧŪÔÚÁ―ģĮĘÐÍâŌÔ
ĢŽÏÖžÆŧŪÔÚÁ―ģĮĘÐÍâŌÔ![]() ΊֹūķĩÄ°ëÔē
ΊֹūķĩÄ°ëÔē![]() ÉÏŅĄÔņŌŧĩã
ÉÏŅĄÔņŌŧĩã![]() ―ĻÔėĀŽŧøīĶĀíģĄĢŽÆäķÔģĮĘÐĩÄÓ°ÏėķČÓëËųŅĄĩØĩãĩ―ģĮĘÐĩÄūāĀëÓÐđØĢŽķÔģĮ
―ĻÔėĀŽŧøīĶĀíģĄĢŽÆäķÔģĮĘÐĩÄÓ°ÏėķČÓëËųŅĄĩØĩãĩ―ģĮĘÐĩÄūāĀëÓÐđØĢŽķÔģĮ![]() šÍģĮ
šÍģĮ![]() ĩÄŨÜÓ°ÏėķČΊģĮ
ĩÄŨÜÓ°ÏėķČΊģĮ![]() šÍģĮ
šÍģĮ![]() ĩÄÓ°ÏėķČÖŪšÍĢŽžĮ
ĩÄÓ°ÏėķČÖŪšÍĢŽžĮ![]() ĩãĩ―ģĮ
ĩãĩ―ģĮ![]() ĩÄūāĀëΊ
ĩÄūāĀëΊ![]() ĢŽ―ĻÔÚ
ĢŽ―ĻÔÚ![]() īĶĩÄĀŽŧøīĶĀíģĄķÔģĮ
īĶĩÄĀŽŧøīĶĀíģĄķÔģĮ![]() šÍģĮ
šÍģĮ![]() ĩÄŨÜÓ°ÏėķČΊ
ĩÄŨÜÓ°ÏėķČΊ![]() ĢŽÍģžÆĩũēéąíÃũĢšĀŽŧøīĶĀíģĄķÔģĮ
ĢŽÍģžÆĩũēéąíÃũĢšĀŽŧøīĶĀíģĄķÔģĮ![]() ĩÄÓ°ÏėķČÓëËųŅĄĩØĩãĩ―ģĮ
ĩÄÓ°ÏėķČÓëËųŅĄĩØĩãĩ―ģĮ![]() ĩÄūāĀëĩÄÆ―·―ģÉ·īąČĢŽąČĀýÏĩĘýΊ4ĢŽķÔģĮ
ĩÄūāĀëĩÄÆ―·―ģÉ·īąČĢŽąČĀýÏĩĘýΊ4ĢŽķÔģĮ![]() ĩÄÓ°ÏėķČÓëËųŅĄĩØĩãĩ―ģĮ
ĩÄÓ°ÏėķČÓëËųŅĄĩØĩãĩ―ģĮ![]() ĩÄūāĀëĩÄÆ―·―ģÉ·īąČĢŽąČĀýÏĩĘýΊ
ĩÄūāĀëĩÄÆ―·―ģÉ·īąČĢŽąČĀýÏĩĘýΊ![]() ĢŽĩąĀŽŧøīĶĀíģĄ―ĻÔÚ
ĢŽĩąĀŽŧøīĶĀíģĄ―ĻÔÚ![]() ĩÄÖÐĩãĘąĢŽķÔģĮ
ĩÄÖÐĩãĘąĢŽķÔģĮ![]() šÍģĮ
šÍģĮ![]() ĩÄŨÜÓ°ÏėķČΊ0.065Ģŧ
ĩÄŨÜÓ°ÏėķČΊ0.065Ģŧ
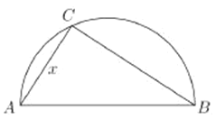
ĢĻ1ĢĐ―Ŧ![]() ąíĘūģÉ
ąíĘūģÉ![]() ĩÄšŊĘýĢŧ
ĩÄšŊĘýĢŧ
ĢĻ2ĢĐÅÐķÏ![]() ÉÏĘĮ·ņīæÔÚŌŧĩãĢŽĘđ―ĻÔÚīËīĶĩÄĀŽŧøīĶĀíģĄķÔģĮ
ÉÏĘĮ·ņīæÔÚŌŧĩãĢŽĘđ―ĻÔÚīËīĶĩÄĀŽŧøīĶĀíģĄķÔģĮ![]() šÍģĮ
šÍģĮ![]() ĩÄŨÜÓ°ÏėķČŨîÐĄ?ČôīæÔÚĢŽĮóģöļÃĩãĩ―ģĮ
ĩÄŨÜÓ°ÏėķČŨîÐĄ?ČôīæÔÚĢŽĮóģöļÃĩãĩ―ģĮ![]() ĩÄūāĀëĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŧ
ĩÄūāĀëĢŧČôēŧīæÔÚĢŽËĩÃũĀíÓÉĢŧ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÖąČýĀâÖųABCĐA1B1C1ĢĻēāĀâīđÖąÓÚĩŨÃæĩÄĀâÖųĢĐÖÐĢŽCAĄÍCBĢŽCAĢ―CBĢ―CC1Ģ―2ĢŽķŊĩãDÔÚÏßķÎABÉÏĢŪ
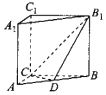
ĢĻ1ĢĐĮóÖĪĢšĩąĩãDΊABĩÄÖÐĩãĘąĢŽÆ―ÃæB1CDĄÍÉÏÆ―ÃæABB1A1Ģŧ
ĢĻ2ĢĐĩąABĢ―3ADĘąĢŽĮóÆ―ÃæB1CDÓëÆ―ÃæBB1C1CËųģÉĩÄČņķþÃæ―ĮĩÄÓāÏŌÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÏÂÁÐÎåļöÃüĖâĢš
ĒŲĄ°![]() ĄąĘĮĄ°
ĄąĘĮĄ°![]() ΊRÉÏĩÄÔöšŊĘýĄąĩÄģä·ÖēŧąØŌŠĖõžþĢŧ
ΊRÉÏĩÄÔöšŊĘýĄąĩÄģä·ÖēŧąØŌŠĖõžþĢŧ
ĒÚšŊĘý![]() ÓÐÁ―ļöÁãĩãĢŧ
ÓÐÁ―ļöÁãĩãĢŧ
ĒÛžŊšÏ![]() ĢŽ
ĢŽ![]() ĢŽīÓAĢŽBÖÐļũČÎŌâČĄŌŧļöĘýĢŽÔōÕâÁ―ĘýÖŪšÍĩČÓÚ4ĩÄļÅÂĘĘĮ
ĢŽīÓAĢŽBÖÐļũČÎŌâČĄŌŧļöĘýĢŽÔōÕâÁ―ĘýÖŪšÍĩČÓÚ4ĩÄļÅÂĘĘĮ![]() Ģŧ
Ģŧ
ĒÜķŊÔēCžČÓëķĻÔē![]() ÏāÍâĮÐĢŽÓÖÓëyÖáÏāĮÐĢŽÔōÔēÐÄCĩÄđėžĢ·―ģĖĘĮ
ÏāÍâĮÐĢŽÓÖÓëyÖáÏāĮÐĢŽÔōÔēÐÄCĩÄđėžĢ·―ģĖĘĮ![]() Ģŧ
Ģŧ
ĒÝČôķÔČÎŌâĩÄÕýĘýxĢŽēŧĩČĘ―![]() šãģÉÁĒĢŽÔōĘĩĘýaĩÄČĄÖĩ·ķΧĘĮ
šãģÉÁĒĢŽÔōĘĩĘýaĩÄČĄÖĩ·ķΧĘĮ![]() .
.
ÆäÖÐÕýČ·ĩÄÃüĖâÐōšÅĘĮ________ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋ―ŦšėĄĒšÚĄĒĀķĄĒ°Ũ5ÕÅÖ―ÅÆĢĻÆäÖаŨÖ―ÅÆÓÐ2ÕÅĢĐËæŧú·Ö·ĒļøžŨĄĒŌŌĄĒąûĄĒķĄ4ļöČËĢŽÃŋČËÖÁÉŲ·ÖĩÃ1ÕÅĢŽÔōÏÂÁÐÁ―ļöĘžþΊŧĨģâĘžþĩÄĘĮĢĻ ĢĐ
A. ĘžþĄ°žŨ·ÖĩÃ1ÕÅ°ŨÅÆĄąÓëĘžþĄ°ŌŌ·ÖĩÃ1ÕÅšėÅÆĄą
B. ĘžþĄ°žŨ·ÖĩÃ1ÕÅšėÅÆĄąÓëĘžþĄ°ŌŌ·ÖĩÃ1ÕÅĀķÅÆĄą
C. ĘžþĄ°žŨ·ÖĩÃ1ÕÅ°ŨÅÆĄąÓëĘžþĄ°ŌŌ·ÖĩÃ2ÕÅ°ŨÅÆĄą
D. ĘžþĄ°žŨ·ÖĩÃ2ÕÅ°ŨÅÆĄąÓëĘžþĄ°ŌŌ·ÖĩÃ1ÕÅšÚÅÆĄą
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com