
【题目】已知双曲线 ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,过左焦点F1(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于P,Q两点,则|PE|+|QE|的值为( )
,过左焦点F1(﹣c,0)作圆x2+y2=a2的切线,切点为E,延长F1E交抛物线y2=4cx于P,Q两点,则|PE|+|QE|的值为( )
A.![]()
B.10a
C.![]()
D.![]()
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】圆心在y轴上,半径为1,且过点(1,2)的圆的方程为( )
A.x2+(y﹣2)2=1
B.x2+(y+2)2=1
C.(x﹣1)2+(y﹣3)2=1
D.x2+(y﹣3)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等边三角形ABC与正方形ABDE有一公共边AB,二面角C﹣AB﹣D的余弦值为 ![]() ,M,N分别是AC.BC的中点,则EM,AN所成角的余弦值等于( )
,M,N分别是AC.BC的中点,则EM,AN所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=2 ![]() ,AA1=
,AA1= ![]() ,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
(Ⅱ)求二面角B﹣A1D﹣C的大小.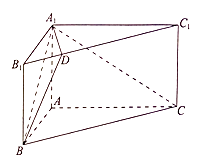
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点M(x,y)与两个定点M1(26,1),M2(2,1)的距离之比等于5.
(1)求点M的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为C,过点A(﹣2,3)的直线l被C所截得的线段的长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,且右准线方程为x=5.
,且右准线方程为x=5.
(1)求椭圆方程;
(2)过椭圆右焦点F作斜率为1的直线l与椭圆C交于A,B两点,P为椭圆上一动点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为B,C,D).当返回舱距地面1万米的P点时(假定以后垂直下落,并在A点着陆),C救援中心测得飞船位于其南偏东60°方向,仰角为60°,B救援中心测得飞船位于其南偏西30°方向,仰角为30°.D救援中心测得着陆点A位于其正东方向.
(1)求B,C两救援中心间的距离;
(2)D救援中心与着陆点A间的距离.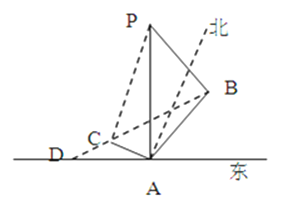
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且 ![]() ,如图.
,如图.
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E﹣AC﹣D的正切值.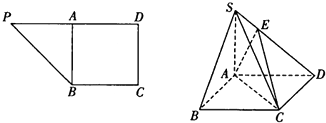
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com