
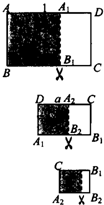
 长为1,宽为a($\frac{1}{2}$<a<1)的矩形纸片,剪下一个边长等于矩形宽度的正方形(称为第1次操作),剩下矩形长为原矩形的宽,如图,再剪下一个边长等于此时矩形宽度的正方形(称为第2次操作),剩下矩形长为第二个矩形的宽,如此反复操作下去,若在第n次操作后,剩下的矩形为正方形,则操作终止.
长为1,宽为a($\frac{1}{2}$<a<1)的矩形纸片,剪下一个边长等于矩形宽度的正方形(称为第1次操作),剩下矩形长为原矩形的宽,如图,再剪下一个边长等于此时矩形宽度的正方形(称为第2次操作),剩下矩形长为第二个矩形的宽,如此反复操作下去,若在第n次操作后,剩下的矩形为正方形,则操作终止.分析 (1)求出n=1,2,3时,剩下矩形的长和宽,即可得到n的最大值;
(2)求出数列{an}的前n项,再将n-2个式子相加,可得Sn=2+a-an-1,再结合a的范围和不等式的性质,即可得证.
解答 解:(1)当n=1时,即进行第一次操作后,剩下矩形的长为a=$\frac{3}{5}$,
此时矩形的宽为1-$\frac{3}{5}$=$\frac{2}{5}$;
当n=2时,即进行第二次操作后,剩下矩形的长为$\frac{2}{5}$,
此时矩形的宽为$\frac{3}{5}$-$\frac{2}{5}$=$\frac{1}{5}$;
当n=3时,即进行第三次操作后,剩下矩形的长为$\frac{1}{5}$,
此时矩形的宽为$\frac{2}{5}$-$\frac{1}{5}$=$\frac{1}{5}$.
依题意,此时操作停止,
故所求正整数n的最小值为3;
(2)证明:由题意,可得数列{an}满足a1=1,a2=a,a3=a1-a2,
a4=a2-a3,…,an=an-2-an-1,(n≥3,n∈N),
将以后n-2个式子相加,可得
Sn-a1-a2=a1-an-1,即Sn-1-a=1-an-1,
则Sn=2+a-an-1,
由$\frac{1}{2}$<a<1,则当n≥3时,0<an-1<a<1,
即有a+2-an-1<2+a<2+1=3,
又2+a-an-1>2+a-a=2,
则有2<Sn<3.
点评 本题考查操作型的应用题的解法,考查数列的求和方法:累加法和相消求和,考查不等式的性质,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象关于直线$x=\frac{5}{8}π$对称 | |
| B. | f(x)的图象关于点($-\frac{3}{8}π$,0)对称 | |
| C. | 若f(x1)=f(x2),则x1-x2=kπ,k∈Z | |
| D. | f(x)的图象向右平移$\frac{π}{4}$个单位长度后得$g(x)=\sqrt{2}sin(2x+\frac{π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{x\left|{x<\frac{1}{2}}\right.}\right\}$ | B. | $\left\{{x\left|{x>\frac{1}{2}}\right.}\right\}$ | C. | {x|x≥-1} | D. | {x|x<3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com