
分析 (1)若x∈A,则x=f(x)成立,则f[f(x)]=f(x)=x必成立,进而根据集合包含关系的定义,得到结论;
(2)由A={x|f(x)=x}={x|x2+ax+b=x}={x|x2+(a-1)x+b=0}={-1,3},结合方程根与系数关系可求a,b,进而可求,f(x),然后代入B={x|f[f(x)]=x}整理可求.
解答 (1)证明:若x∈A,则x=f(x)成立,
则f[f(x)]=f(x)=x必成立,即x∈B,
故A⊆B;
(2)解:∵A={x|f(x)=x}={x|x2+ax+b=x}={x|x2+(a-1)x+b=0}={-1,3},
∴-1,3是方程x2+(a-1)x+b=0的根,
∴$\left\{\begin{array}{l}{1-a=2}\\{b=-3}\end{array}\right.$,即a=-1,b=-3,
∴f(x)=x2-x-3,
∴B={x|f[f(x)]=x}={x|f(x2-x-3)=x}={x|(x2-x-3)2-(x2-x-3)-3=x},
化简可得,(x2-x-3)2-x2=0,
∴(x2-3)(x2-2x-3)=0,
∴x=$\sqrt{3}$或x=-$\sqrt{3}$或x=3或x=-1,
∴B={$\sqrt{3}$,-$\sqrt{3}$,-1,3}.
点评 本题主要考查了二次函数与二次方程之间关系的相互转化,方程的根与系数关系的应用


科目:高中数学 来源: 题型:选择题
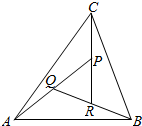 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )| A. | $\frac{2}{7},\frac{4}{7}$ | B. | $\frac{1}{2},\frac{1}{4}$ | C. | $\frac{1}{6},\frac{2}{7}$ | D. | $\frac{1}{6},\frac{3}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>1 | B. | $k>\frac{1}{3}$ | C. | $k>\frac{1}{5}$ | D. | $k>\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com