
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知(sinB+sinC)(b﹣c)=(sinA+sinC)a.
(1)求B;
(2)已知b=4,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
【答案】(1) B![]() .(2) 2
.(2) 2![]() 4.
4.
【解析】
(1)利用正弦定理得到a2+c2﹣b2=﹣ac,再利用余弦定理得到![]() ,解得答案.
,解得答案.
(2)根据面积公式计算得到ac=4,再利用余弦定理得到a+c=2![]() ,得到周长.
,得到周长.
(1)∵(sinB+sinC)(b﹣c)=(sinA+sinC)a,
∴由正弦定理可得:(b+c)(b﹣c)=(a+c)a,∴a2+c2﹣b2=﹣ac,
∴cosB![]() ,∵B∈(0,π),∴B
,∵B∈(0,π),∴B![]() .
.
(2)∵b=4,B![]() ,△ABC的面积为
,△ABC的面积为![]() acsinB
acsinB![]() ac,∴解得ac=4,
ac,∴解得ac=4,
由余弦定理b2=a2+c2﹣2accosB,可得16=a2+c2+ac=(a+c)2﹣ac=(a+c)2﹣4
解得a+c=2![]() , ∴△ABC的周长a+c+b=2
, ∴△ABC的周长a+c+b=2![]() 4.
4.


科目:高中数学 来源: 题型:
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年 份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额(万元) | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长(万元) | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)请用最小二乘法求出y关于x的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额是8万元,估计该公司在该年的年利润增长是多少?(结果保留2位小数)
(2)现从2012—2018年这7年中抽取2年进行调查,记![]() =年利润增长-投资金额,求这两年都是
=年利润增长-投资金额,求这两年都是![]() >2(万元)的概率.
>2(万元)的概率.
参考公式:回归方程![]() 中,
中, 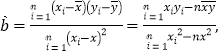
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a1,a3,a13成等比数列,若a1=1,Sn为数列{an}的前n项和,则![]() 的最小值为( )
的最小值为( )
A.4B.3C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某竞赛的题库系统有60%的自然科学类题目,40%的文化生活类题目(假设题库中的题目总数非常大),参赛者需从题库中抽取3个题目作答,有两种抽取方法:方法一是直接从题库中随机抽取3个题目;方法二是先在题库中按照题目类型用分层抽样的方法抽取10个题目作为样本,再从这10个题目中任意抽取3个题目.
(1)两种方法抽取的3个题目中,恰好有1个自然科学类题目和2个文化生活类题目的概率是否相同?若相同,说明理由;若不同,分别计算出两种抽取方法对应的概率.
(2)已知某参赛者抽取的3个题目恰好有1个自然科学类题目和2个文化生活类题目,且该参赛者答对自然科学类题目的概率为![]() ,答对文化生活类题目的概率为
,答对文化生活类题目的概率为![]() .设该参赛者答对的题目数为X,求X的分布列和数学期望.
.设该参赛者答对的题目数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M到定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(1)求动点M的轨迹方程;
(2)令(1)中方程表示曲线C,点S(2,0),过点B(1,0)的直线l与曲线C相交于P,Q两点,求△PQS的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA=PD![]() ,四边形ABCD为等腰梯形,BC∥AD,BC=CD
,四边形ABCD为等腰梯形,BC∥AD,BC=CD![]() AD=1,E为PA的中点.
AD=1,E为PA的中点.
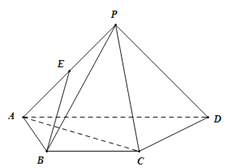
(1)求证:EB∥平面PCD;
(2)求平面PAC与平面PCD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是我国南北朝时代的伟大科学家,在数学上有突出贡献,他在实践的基础上提出了体积计算原理(祖暅原理):“幂势既同,则积不容异.”教材中的“探究与发现”利用祖暅原理将半球的体积转化为一个圆柱与一个圆锥的体积之差,从而得出球的体积计算公式.如图(1)是一种“四脚帐篷”的示意图,用任意平行于帐篷底面![]() 的平面截帐篷,得截面四边形为正方形,该帐篷的三视图如图(2)所示,其中正视图的投影线方向垂直于平面
的平面截帐篷,得截面四边形为正方形,该帐篷的三视图如图(2)所示,其中正视图的投影线方向垂直于平面![]() ,正视图和侧视图中的曲线均为半径为1的半圆.模仿上述球的体积计算方法,得该帐篷的体积为( ).
,正视图和侧视图中的曲线均为半径为1的半圆.模仿上述球的体积计算方法,得该帐篷的体积为( ).
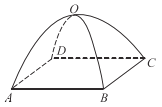
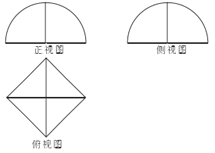
图(1) 图(2)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com