Question

在等差数列{a_n}中，a₁，a₃，a₄成等比数列，则该等比数列的公比为________．

Answer 1

，或1
分析：设等差数列{a_n}公差为d，由条件可得（a₁+2d）²=a₁（a₁+3d），解得 d=0 或a₁=-4d，在这两种情况下，分别求出公比的值．
解答：设等差数列{a_n}公差为d，∵a₁，a₃，a₄成等比数列，
∴a₃²=a₁a₄，即 （a₁+2d）²=a₁（a₁+3d），解得 d=0 或a₁=-4d．
若 d=0，则等比数列的公比q=1．
若a₁=-4d，则等比数列的公比q===．
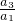
故答案为 ，或1．
点评：本题主要考查等比数列的定义和性质，等差数列的通项公式，求出d=0 或a₁=-4d，是解题的关键，属于基础题．