【题目】已知椭圆
，椭圆
经过椭圆C1的左焦点F 和上下顶点A，B.设斜率为k的直线l与椭圆C2相切，且与椭圆C1交于P，Q两点.
（1）求椭圆C2的方程；
（2）①若
，求k的值；
②求PQ弦长最大时k的值.
【答案】（1）
；（2）①
；②
.
【解析】
（1）分别求出C1的左焦点与上下顶点的坐标，可得椭圆C2的
的值，可得椭圆C2的方程；
（2）①设直线l的方程为
与椭圆C2联立，由直线
与椭圆
相切，可得
，
可得
的关系，同时直线l与椭圆C1的方程联立，
，
，由韦达定理结合
，即
，代入可得k的值；
②由①知
，可得
关于
的函数，化简利用基本不等式可得PQ弦长最大时k的值.
解：（1）由题意可知，椭圆C1的左焦点
，
上下顶点
，
，
所以椭圆C2的左顶点为，上下顶点，，
所以
，
，
所以椭圆C2的方程为.
（2）设直线l的方程为与椭圆C2：方程联立，消去y得，
，
因为直线与椭圆相切，所以
，
整理得，
，
直线l与椭圆C1的方程联立得，
，
其中
.
设，，
则
.
①因为，所以，
即
，
所以
.
②由①知
，
设
，则
.
所以当
时，PQ的长最大，最大值为.
三点一测快乐周计划系列答案科目：高中数学 来源： 题型：
【题目】某学校有40名高中生参加足球特长生初选，第一轮测身高和体重，第二轮足球基础知识问答，测试员把成绩（单位：分）分组如下：第1组
，第2组
，第3组
，第4组
，第5组
，得到频率分布直方图如图所示.
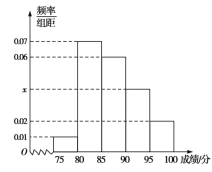
（1）根据频率分布直方图估计成绩的平均值（同一组中的数据用该组区间的中点值作代表）；
（2）用分层抽样的方法从成绩在第3，4，5组的高中生中抽取6名组成一个小组，若再从这6人中随机选出2人担任小组负责人，求这2人来自第3，4组各1人的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，一隧道内设双行线公路，其截面由一个长方形和抛物线构成．为保证安全，要求行使车辆顶部（设为平顶）与隧道顶部在竖直方向上的高度之差至少要有0.5米．若行车道总宽度AB为6米，则车辆通过隧道的限制高度是______米（精确到0.1米）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线Γ的准线方程为
.焦点为
.
（1）求证：抛物线Γ上任意一点
的坐标
都满足方程：
（2）请求出抛物线Γ的对称性和范围，并运用以上方程证明你的结论；
（3）设垂直于
轴的直线与抛物线交于
两点，求线段
的中点
的轨迹方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某部门共有4名员工， 某次活动期间， 周六、 周日的上午、 下午各需要安排一名员工值班，若规定同一天的两个值班岗位不能安排给同一名员工， 则该活动值班岗位的不同安排方式共有（ ）
A.120种B.132种C.144种D.156种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四个命题：
函数
的最大值为1；
“
，
”的否定是“
”；
若
为锐角三角形，则有
；
“
”是“函数
在区间
内单调递增”的充分必要条件．
其中错误的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《算法统宗》全称《新编直指算法统宗》，是屮国古代数学名著，程大位著.书中有如下问题：“今有五人均银四十两，甲得十两四钱，戊得五两六钱.问：次第均之，乙丙丁各该若干？”意思是：有5人分40两银子，甲分10两4钱，戊分5两6钱，且相邻两项差相等，则乙丙丁各分几两几钱？（注：1两等于10钱）（ ）
A.乙分8两，丙分8两，丁分8两B.乙分8两2钱，丙分8两，丁分7两8钱
C.乙分9两2钱，丙分8两，丁分6两8钱D.乙分9两，丙分8两，丁分7两
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
