
已知实数a,b满足 ,则函数f(x)=
,则函数f(x)=  的两个极值点都在(0,1)内的概率为______
的两个极值点都在(0,1)内的概率为______

解析试题分析:本题考查的知识点是几何概型的意义,关键是要找出函数f(x)=  有极值对应的可行域面积的大小和实数a,b满足
有极值对应的可行域面积的大小和实数a,b满足 对应的图形面积的大小。
对应的图形面积的大小。
∵函数f(x)=  ∴f′(x)=x2-2ax+b,
∴f′(x)=x2-2ax+b,
∵函数f(x)=  的两个极值点都在(0,1)内,
的两个极值点都在(0,1)内,
x2-2ax+b=0的两个根都在(0,1)内,
∴两根之和2a∈(0,2),两根之积b∈(0,1),
∴△=4a2-4b>0,0<a<1,0<b<1∵实数a,b满足 ,
,
∴如图所示,区域-1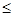 a
a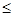 1,-1
1,-1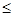 b
b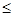 1的面积(图中正方形所示)为4,
1的面积(图中正方形所示)为4,
a2>b在条件0<a<1,0<b<1下的面积(图中阴影所示)为 ,所求的概率为
,所求的概率为
考点:几何概型
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、含面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式求解.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:填空题
某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下:如果出现两个偶数或两个奇数,就将两数相加的和记为 ;如果出现一奇一偶,则将它们的差的绝对值记为
;如果出现一奇一偶,则将它们的差的绝对值记为 ,则随机变量
,则随机变量 的数学期望为 .
的数学期望为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在平面直角坐标系 中,设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E是到原点的距离不大于1的点构成的区域,向D中随机投一点,则所投点在E中的概率是
中,设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E是到原点的距离不大于1的点构成的区域,向D中随机投一点,则所投点在E中的概率是 
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)骰子四个面上分别标有1,2,3,4这四个数字,抛掷这颗正四面体骰子,观察抛掷后能看到的数字.若连续抛掷两次,两次朝下面上的数字之积大于6的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com