
已知数列{an}中,a2=1,前n项和为Sn,且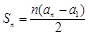 .
.
(1)求a1,a3;
(2)求证:数列{an}为等差数列,并写出其通项公式;
(3)设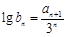 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
(1) a1=S1=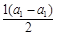 ="0," a3=2
="0," a3=2
(2) an=n-1
(3) 存在唯一正整数数 对(p,q)=(2,3),使b1,bp,bq成等比数列
解析试题分析:解:(1)令n=1,则a1=S1=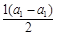 =0. 2分; a3=2; 3分
=0. 2分; a3=2; 3分
(2)由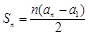 ,即
,即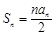 , ① 得
, ① 得 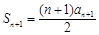 . ②
. ②
②-①,得 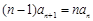 . ③ 5分
. ③ 5分
于是,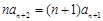 . ④
. ④
③+④,得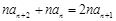 ,即
,即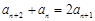 . 7分
. 7分
又a1=0,a2=1,a2-a1=1,
所以,数列{an}是以0为首项,1为公差的等差数列.
所以,an=n-1. 9分
法二②-①,得 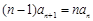 . ③ 5分
. ③ 5分
于是,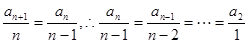 7分
7分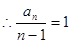 所以,an=n-1. 9分
所以,an=n-1. 9分
(3)假设存在正整数数组(p,q),使b1,bp,bq成等比数列,
则lgb1,lgbp,lgbq成等差数列, 10分
于是,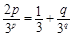 . 11分
. 11分
所以,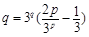 (☆).易知(p,q)=(2,3)为方程(☆)的一组解. 12分
(☆).易知(p,q)=(2,3)为方程(☆)的一组解. 12分
当p≥3,且p∈N*时,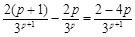 <0,
<0,
故数列{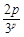 }(p≥3)为递减数列 14分
}(p≥3)为递减数列 14分
于是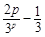 ≤
≤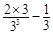 <0,所以此时方程(☆)无正整数解. 15分
<0,所以此时方程(☆)无正整数解. 15分
综上,存在唯一正整数数 对(p,q)=(2,3),使b1,bp,bq成等比数列. 16分
考点:等差数列和等比数列
点评:解决的关键是根据等差数列和等比数列的性质以及定义来求解运用。属于基础题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
下图是一个按照某种规律排列出来的三角形数阵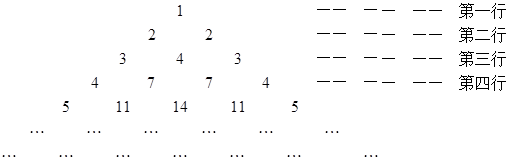
假设第 行的第二个数为
行的第二个数为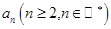
(1)依次写出第七行的所有7个数字(不必说明理由);
(2)写出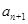 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出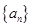 的通项公式
的通项公式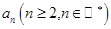 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线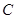 :
: ,数列
,数列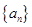 的首项
的首项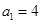 ,且
,且
当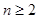 时,点
时,点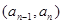 恒在曲线
恒在曲线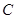 上,数列{
上,数列{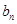 }满足
}满足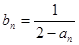
(1)试判断数列 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列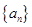 和
和 的通项公式;
的通项公式;
(3)设数列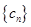 满足
满足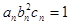 ,试比较数列
,试比较数列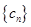 的前
的前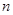 项和
项和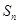 与
与 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com