
【题目】华罗庚中学高二排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:![]() )分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:
)分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:![]() )分别是:170、159、162、173、181、165、176、168、178、179.
)分别是:170、159、162、173、181、165、176、168、178、179.
(1)请根据两队身高数据作出茎叶图,并分析指出哪个队的身高数据方差较小(无需计算)以及排球队的身高数据的中位数与众数;
(2)现从两队所有身高超过![]() 的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
【答案】(1)茎叶图见解析,篮球队的身高数据方差较小.排球队的身高数据中位数为169,众数168
(2)![]()
【解析】
(1)根据已知数据可画出茎叶图;根据茎叶图可知篮球队的身高数据更集中,可知方差较小;由中位数和众数的定义可求得结果;
(2)利用列举法可得到所有基本事件个数和满足题意的基本事件个数,由古典概型概率公式可求得结果.
(1)茎叶图如图所示:
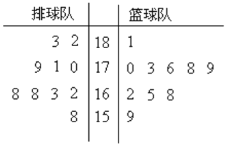
由茎叶图可知,排球队的平均身高为![]() ,篮球队的平均身高为
,篮球队的平均身高为![]() ,可知篮球队的身高在平均数附近的集中程度高于排球队的集中程度,由此可知:篮球队的身高数据方差较小.
,可知篮球队的身高在平均数附近的集中程度高于排球队的集中程度,由此可知:篮球队的身高数据方差较小.
将排球队的数据按从小到大数据排列,则中位数为:![]() ,
,
![]() 排球队身高数据中,
排球队身高数据中,![]() 个数最多,则众数
个数最多,则众数![]() .
.
(2)两队所有身高超过![]() 的同学恰有
的同学恰有![]() 人,其中
人,其中![]() 人来自排球队,记为
人来自排球队,记为![]() ,
,![]() 人来自篮球队,记为
人来自篮球队,记为![]() ,则从
,则从![]() 人中抽取
人中抽取![]() 名同学的基本事件为:
名同学的基本事件为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 个;
个;
其中恰好两人来自排球队一人来自篮球队所含的事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 个,
个,
![]() 恰好两人来自排球队,一人来自篮球队的概率
恰好两人来自排球队,一人来自篮球队的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为椭圆
为椭圆![]() 上任意一点,且
上任意一点,且![]() 的最小值为0.
的最小值为0.
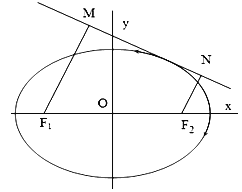
(1)求椭圆![]() 的方程;
的方程;
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() ,
,![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
,![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2017年1月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论正确的是( )
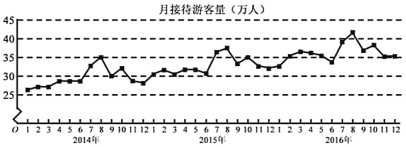
A.月接待游客逐月增加
B.年接待游客量逐年减少
C.各年的月接待游客量高峰期大致在6、7月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性较小,变化比较稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近两年来,以《中国诗词大会》为代表的中国文化类电视节目带动了一股中国文化热潮.某台举办闯关答题比赛,共分两轮,每轮共有4类题型,选手从前往后逐类回答,若中途回答错误,立马淘汰,若全部回答正确,就能获得一枚复活币并进行下一轮答题,两轮都通过就可以获得最终奖金.选手在第一轮闯关获得的复活币,系统会在下一轮答题中自动使用,即下一轮重新进行闯关答题时,在某一类题型中回答错误,自动复活一次,视为答对该类题型.若某选手每轮的4类题型的通过率均分别为![]() 、
、![]() 、
、![]() 、
、![]() ,则该选手进入第二轮答题的概率为_________;该选手最终获得奖金的概率为_________.
,则该选手进入第二轮答题的概率为_________;该选手最终获得奖金的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了![]() 位医护人员的关爱患者考核分数(患者考核:
位医护人员的关爱患者考核分数(患者考核:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:
表示;医护专业知识考核分数(试卷考试:![]() 分制),用相关的特征量
分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到
的线性回归方程(计算结果精确到![]() );
);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计当某医护人员的医护专业知识考核分数为![]() 分时,他的关爱患者考核分数(精确到
分时,他的关爱患者考核分数(精确到![]() ).
).
参考公式及数据:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接国庆汇演,学校拟对参演的班级进行奖励性加分表彰,每选中一个节目,其班级量化考核积分加3分.某班级准备了三个文娱节目,这三个节目被选中的概率分别为![]() ,
,![]() ,
,![]() ,且每个节目是否被选中是相互独立的.
,且每个节目是否被选中是相互独立的.
(1)求该班级被加分的概率;
(2)求该班级获得奖励性积分![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com