
【题目】已知椭圆G:![]() ,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
,过点A(0,5),B(﹣8,﹣3),C、D在该椭圆上,直线CD过原点O,且在线段AB的右下侧.
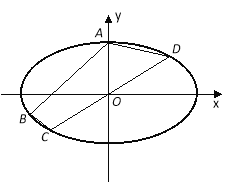
(1)求椭圆G的方程;
(2)求四边形ABCD 的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)先将点A(0,5),B(-8,3),代入椭圆的方程解得:a=10 b=5,最后写出椭圆G的方程;(2)连OB,则四边形ABCD的面积![]() ,
,![]() 分别表示A,B到直线CD的距离,设CD:-kx+y=0,代入椭圆方程消去y得到关于x的一元二次方程,再结合求根公式即可求得四边形ABCD的面积,最后结合基本不等式求最大值,从而解决问题
分别表示A,B到直线CD的距离,设CD:-kx+y=0,代入椭圆方程消去y得到关于x的一元二次方程,再结合求根公式即可求得四边形ABCD的面积,最后结合基本不等式求最大值,从而解决问题
试题解析:(1)将点A(0,5),B(﹣8,﹣3)代入椭圆G 的方程解得:
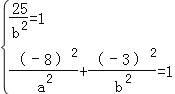 ,解得:a2=100,b2=25.
,解得:a2=100,b2=25.
∴椭圆G的方程为:![]() ;
;
(2)连结OB,
则![]() ,---7分
,---7分
其中dA,dB分别表示点A,点B 到直线CD 的距离.
设直线CD方程为y =kx,代入椭圆方程![]() ,得x2+4k2x2﹣100=0,
,得x2+4k2x2﹣100=0,
解得:![]() ,
,
∴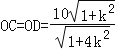 ,
,
又![]() ,
,![]() ,
,
则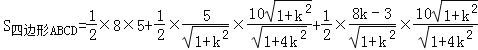
=![]() .
.
当且仅当k=1时 取等号。


 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为![]() ,鲑鱼的耗氧量的单位数为
,鲑鱼的耗氧量的单位数为![]() ,研究中发现
,研究中发现![]() 与
与![]() 成正比,且当
成正比,且当![]() 时,
时, ![]() .
.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)计算一条鲑鱼的游速是![]() 时耗氧量的单位数;
时耗氧量的单位数;
(3)当鲑鱼的游速增加![]() 时,其耗氧量是原来的几倍?
时,其耗氧量是原来的几倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
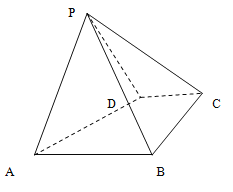
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与圆C:
与圆C:![]() 相交于A,B两点,弦AB中点为M(0,1),
相交于A,B两点,弦AB中点为M(0,1),
(1)求实数![]() 的取值范围以及直线
的取值范围以及直线![]() 的方程;
的方程;
(2)若圆C上存在四个点到直线![]() 的距离为
的距离为![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)已知N(0,﹣3),若圆C上存在两个不同的点P,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径![]()
,此时圆内接正六边形的周长为![]()
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据: ![]()
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列5个命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x+1<0,则綈p:x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则线性回归方程为![]() =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为![]() ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com