
【题目】设![]() 、
、![]() 、
、![]() 是集合,称
是集合,称![]() 为有序三元组,如果集合
为有序三元组,如果集合![]() 、
、![]() 、
、![]() 满足
满足![]()
![]() ,且
,且![]() ,则称有序三元组
,则称有序三元组![]() 为最小相交(其中
为最小相交(其中![]() 表示集合
表示集合![]() 中的元素个数),如集合
中的元素个数),如集合![]() ,
,![]() ,
,![]() 就是最小相交有序三元组,则由集合
就是最小相交有序三元组,则由集合![]() 的子集构成的最小相交有序三元组的个数是________
的子集构成的最小相交有序三元组的个数是________
【答案】7680
【解析】
令S={1,2,3,4,5,6},由题意知,必存在两两不同的x,y,z∈S,使得A∩B={x},B∩C={y},C∩A={z},而要确定x,y,z共有6×5×4种方法;对S中剩下的3个元素,每个元素有4种分配方式,即可得到最小相交的有序三元组(A,B,C)的个数.
令S={1,2,3,4,5,6},如果(A,B,C)是由S的子集构成的最小相交的有序三元组,则存在两两不同的x,y,z∈S,使得A∩B={x},B∩C={y},C∩A={z},(如图),要确定x,y,z共有6×5×4种方法;
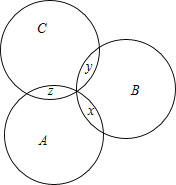
对S中剩下的3个元素,每个元素有4种分配方式,即它属于集合A,B,C中的某一个或不属于任何一个,则有43种确定方法.
所以最小相交的有序三元组(A,B,C)的个数6×5×4×43=7680.
故答案为:7680


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知甲、乙、丙三位同学在某次考试中总成绩列前三名,有![]() ,
,![]() ,
,![]() 三位学生对其排名猜测如下:
三位学生对其排名猜测如下:![]() :甲第一名,乙第二名;
:甲第一名,乙第二名;![]() :丙第一名;甲第二名;
:丙第一名;甲第二名;![]() :乙第一名,甲第三名.成绩公布后得知,
:乙第一名,甲第三名.成绩公布后得知,![]() ,
,![]() ,
,![]() 三人都恰好猜对了一半,则第一名是__________.
三人都恰好猜对了一半,则第一名是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示:
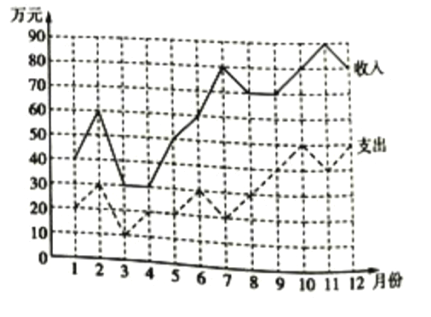
根据该折线图可知,下列说法错误的是( )
A. 该超市2018年的12个月中的7月份的收益最高
B. 该超市2018年的12个月中的4月份的收益最低
C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益
D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元
查看答案和解析>>
科目:高中数学 来源: 题型:
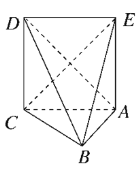
【题目】如图,在三棱锥D-ABC中,![]() 底面ABC,
底面ABC,![]() 为正三角形,若
为正三角形,若![]() ,
,![]() ,则三棱锥D-ABC与三棱锥E-ABC的公共部分构成的几何体的外接球的体积为( )
,则三棱锥D-ABC与三棱锥E-ABC的公共部分构成的几何体的外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:①若
有下述四个结论:①若![]() ,则
,则![]() ;②
;②![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的图象向右平移
的图象向右平移![]() 个单位长度后所得图象关于
个单位长度后所得图象关于![]() 轴对称.其中所有正确结论的编号是( )
轴对称.其中所有正确结论的编号是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月郑州市被国务院确定为全国46个生活垃圾分类处理试点城市之一,此后由郑州市城市管理局起草公开征求意见,经专家论证,多次组织修改完善,数易其稿,最终形成《郑州市城市生活垃圾分类管理办法》(以下简称《办法》).《办法》已于2019年9月26日被郑州市人民政府第35次常务会议审议通过,并于2019年12月1日开始施行.《办法》中将郑州市生活垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他垃圾4类.为了获悉高中学生对垃圾分类的了解情况,某中学设计了一份调查问卷,500名学生参加测试,从中随机抽取了100名学生问卷,记录他们的分数,将数据分成7组:![]() ,
,![]() ,…,
,…,![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
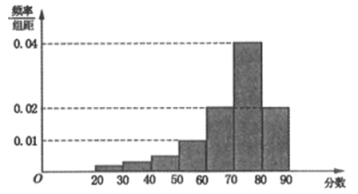
(1)从总体的500名学生中随机抽取一人,估计其分数不低于60的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的学生人数,
内的学生人数,
(3)学校环保志愿者协会决定组织同学们利用课余时间分批参加“垃圾分类,我在实践”活动,以增强学生的环保意识.首次活动从样本中问卷成绩低于40分的学生中随机抽取2人参加,已知样本中分数小于40的5名学生中,男生3人,女生2人,求抽取的2人中男女同学各1人的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
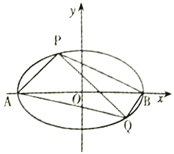
【题目】如图,已知椭圆![]() ,
,![]() 为椭圆的左右顶点,焦点
为椭圆的左右顶点,焦点![]() 到短轴端点的距离为2,且
到短轴端点的距离为2,且![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,直线
的两点,直线![]() 的斜率等于直线
的斜率等于直线![]() 斜率的2倍.
斜率的2倍.
(1)求直线![]() 与直线
与直线![]() 的斜率乘积值;
的斜率乘积值;
(2)求证:直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(3)求三角形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,点
,点![]() 满足
满足![]() ,设倾斜角为
,设倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 为何值时,
为何值时,![]() 最大?求出此最大值.
最大?求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com