
设 为随机变量,从棱长为1的正方体ABCD?A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD?A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积.
(1)求概率P( =0);
=0);
(2)求 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).
(1)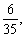
(2)
|
|
|
|
|
|
|
|

【解析】
试题分析:(1)求概率P( = 0),就是求四点共面时概率.古典概型概率
= 0),就是求四点共面时概率.古典概型概率 的求法,关键要找出
的求法,关键要找出 所包含的基本事件个数,然后套用公式
所包含的基本事件个数,然后套用公式
 (2)求
(2)求 的数学期望的基本步骤:首先理解
的数学期望的基本步骤:首先理解 的意义,写出
的意义,写出 可能取的全部值,本题考虑四个顶点不同位置,求体积;其次求
可能取的全部值,本题考虑四个顶点不同位置,求体积;其次求 取各个值的概率,写出概率分布;最后根据概率分布,由数学期望的定义求出
取各个值的概率,写出概率分布;最后根据概率分布,由数学期望的定义求出
试题解析:(1)从正方体的八个顶点中任取四个点,共有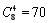 种不同取法.
种不同取法.
其中共面的情况共有12种(6个侧面,6个对角面).
则 3分
3分
(2)任取四个点,当四点不共面时,四面体的体积只有以下两种情况:
①四点在相对面且异面的对角线上,体积为
这样的取法共有2种. 5分
②四点中有三个点在一个侧面上,另一个点在相对侧面上,体积为
这样的取法共有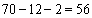 种 7分
种 7分
 的分布列为
的分布列为
|
|
|
|
|
|
|
|
8分
数学期望 10分
10分
考点:概率,数学期望,随机变量的概率分布列.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试数学(江苏卷解析版) 题型:解答题
设 为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,
为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,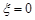 ;当两条棱平行时,
;当两条棱平行时, 的值为两条棱之间的距离;当两条棱异面时,
的值为两条棱之间的距离;当两条棱异面时, .
.
(1)求概率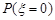 ;
;
(2)求 的分布列,并求其数学期望
的分布列,并求其数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省武汉六中高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012年江苏省高考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com