
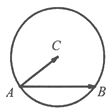
【题目】如图,定圆C半径为2,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且| ![]() |
| ![]() |对任意t∈(0,+∞)恒成立,则
|对任意t∈(0,+∞)恒成立,则 ![]() = .
= . 
科目:高中数学 来源: 题型:
【题目】已知下面四个命题: (1.)从匀速传递的产品生产流水线上,质检员每15分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样;
(2.)两个随机变量相关性越强,则相关系数的绝对值越接近于1;
(3.)对分类变量X和Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大;
(4.)在回归直线方程 ![]() =0.4x+12中,当解释变量x每增加一个单位时,预报变量大约增加0.4个单位.
=0.4x+12中,当解释变量x每增加一个单位时,预报变量大约增加0.4个单位.
其中真命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级开设选修课,其中数学选修课开了三个班.选课结束后,有四名选修英语的同学要求改修数学,但数学选修每班至多可再接收两名同学,那么安排好这四名同学的方案有( )
A.72种
B.54种
C.36种
D.18种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°, ![]() ,D为AC上一点,且AD=3DC.
,D为AC上一点,且AD=3DC. 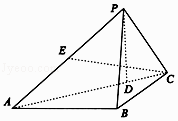
(1)求证:PD⊥平面ABC;
(2)若E为PA中点,求直线CE与平面PAB所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com