科目：高中数学 来源： 题型：解答题
已知函数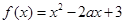
(1)若函数在
的单调递减区间（—∞,2],求函数在区间[3,5]上的最大值.
(2)若函数在在单区间（—∞,2]上是单调递减,求函数
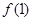的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇.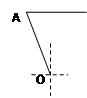
(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行时间应为多少小时？
(Ⅱ)为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值；
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某同学利用暑假时间到一家商场勤工俭学，该商场向他提供了三种付款方式：第一种，每天支付38圆；第二种，第一天付4元，第二天付8元，第三天付12元，以此类推：第三种，第一天付0.4元，以后每天比前一天翻一番（即增加一倍），
你会选择哪种方式领取报酬呢？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分12分）
某公司生产一种电了仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：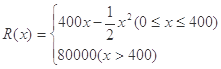
，其中
是仪器的月产量。
⑴将利润表示为月产量的函数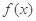
。
⑵当月产量为何值时，公司所获利润最大？最大利润为多少元？（总收益―总成本＝利润）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，当
时，对应
值的集合为
.
的值；（2）若
，求该函数的最值.
.（2）当
时，该函数取得最大值
的零点是－1和3，当
时，
，且
。（1）求该二次函数的解析式；（2）求函数
的最大值。
-4÷
；
.
的不等式
（
，且
）.
,
,其中
是自然常数）.
的单调性和极小值；
在
上单调递增；
.