
 ��ֵ��
��ֵ�� ����֤��
����֤��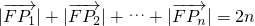 ��
�� =��x1+
=��x1+ ��+��x2+
��+��x2+ ��+��x3+
��+��x3+ ��=x1+x2+x3+3
��=x1+x2+x3+3 =7
=7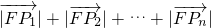 =��x1+1��+��x2+1��+��x3+1��+��+��xn+1��=x1+x2+x3+��+xn+n
=��x1+1��+��x2+1��+��x3+1��+��+��xn+1��=x1+x2+x3+��+xn+n
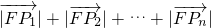 =n+n=2n
=n+n=2n ����֤��
����֤�� ��
�� ����
���� ��
��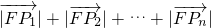 =��x1+
=��x1+ ��+��x2+
��+��x2+ ��+��x3+
��+��x3+ ��+��+��xn+
��+��+��xn+ ��=x1+x2+x3+��+xn+
��=x1+x2+x3+��+xn+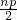

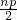
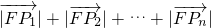 =
=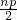 +
+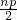 =np
=np ��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4��
��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4��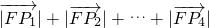 =x1+x2+x3+x4+2p=4p
=x1+x2+x3+x4+2p=4p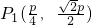 ��
�� ��
��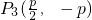 ��
��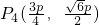 ����
����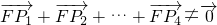
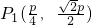 ��
��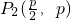 ��
��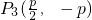 ��
��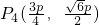 ��һ����n=4ʱ�����������һ��������
��һ����n=4ʱ�����������һ��������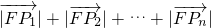 =2n
=2n ����֤��
����֤�� ��
�� ����
���� ��
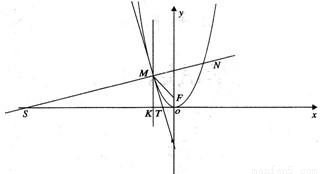
�� ��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4�����������ߵĶ��壬�ɵ�x1+x2+x3+x4=2p���Ӷ��ɵý��ۣ�
��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4�����������ߵĶ��壬�ɵ�x1+x2+x3+x4=2p���Ӷ��ɵý��ۣ�

 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| MF |
| MN |
| PF |
| FA |
| FB |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��0108 ģ���� ���ͣ������
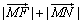 ����СֵΪ4��
����СֵΪ4��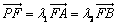 �����жϦ�1+��2�Ƿ�Ϊ��ֵ�����Ƕ�ֵ������ö�ֵ��֤���������Ƕ�ֵ����˵�����ɡ�
�����жϦ�1+��2�Ƿ�Ϊ��ֵ�����Ƕ�ֵ������ö�ֵ��֤���������Ƕ�ֵ����˵�����ɡ� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ģ���� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�갲��ʡ�Ϸ�һ�и߿���ѧ������һ�������ƣ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com