
【题目】已知全集U=R,集合A={x|x2-11x+18<0},B={x|-2≤x≤5}.
(1)求A∩B;B∪(UA);
(2)已知集合C={x|a≤x≤a+2},若C∩![]() =C,求实数a的取值范围.
=C,求实数a的取值范围.
【答案】(1){x|2<x≤5}; {x|x≤5或x≥9}(2)(-∞,-4)∪(5,+∞)
【解析】
(1)化简集合A,根据补集与并集和交集的定义计算即可;(2)根据题意,利用集合的定义与运算性质,列不等式组求出a的取值范围.
(1)集合A={x|x2-11x+18<0}={x|2<x<9},
全集U=R,则UA={x|x≤2或x≥9};
又B={x|-2≤x≤5},则A∩B={x|2<x≤5};
∴B∪(UA)={x|x≤5或x≥9};
(2)集合C={x|a≤x≤a+2},B={x|-2≤x≤5},
则:UB={x|x<-2或x>5},
∵C∩UB=C,
∴CUB,
∴需满足:a+2<-2或a>5,
解得:a<-4或a>5,
所以实数a的取值范围是(-∞,-4)∪(5,+∞).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
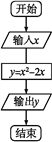
【题目】求函数y=![]() 的值的程序框图如图所示.
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)满足f(﹣x)+f(x)=0且f(x+1)=f(x﹣1),若x∈(0,1)时,f(x)=log2 ![]() ,则y=f(x)在(1,2)内是( )
,则y=f(x)在(1,2)内是( )
A.单调增函数,且f(x)<0
B.单调减函数,且f(x)<0
C.单调增函数,且f(x)>0
D.单调增函数,且f(x)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() f.
f.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,点M和N分别是B1C1和BC的中点.

(1)求证:MB∥平面AC1N;
(2)求证:AC⊥MB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格![]() (元)与时间
(元)与时间![]() (天)组成有序数对
(天)组成有序数对![]() ,点
,点![]() 落在图中的两条线段上;该股票在30天内的日交易量
落在图中的两条线段上;该股票在30天内的日交易量![]() (万股)与时间
(万股)与时间![]() (天)的部分数据如下表所示,且
(天)的部分数据如下表所示,且![]() 与
与![]() 满足一次函数关系,
满足一次函数关系,

第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
那么在这30天中第几天日交易额最大( )
A. 10 B. 15 C. 20 D. 25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com