
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为x万元时,销售量t万件满足t=5- ![]() (其中0
(其中0 ![]() x
x ![]() a,a为正常数),现假定生产量与销售量相等,已知生产该产品t万件还需投入成本(10+2t)万元(不含促销费用),产品的销售价格定为5+
a,a为正常数),现假定生产量与销售量相等,已知生产该产品t万件还需投入成本(10+2t)万元(不含促销费用),产品的销售价格定为5+ ![]() 万元/万件.
万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
【答案】
(1)解:由题意知,利润y=t(5+ ![]() ))﹣(10+2t)﹣x=3t+10-x
))﹣(10+2t)﹣x=3t+10-x
由销售量t万件满足t=5- ![]() (其中0≤x≤a , a为正常数).
(其中0≤x≤a , a为正常数).
代入化简可得:y=25-( ![]() +x),(0≤x≤a , a为正常数)
+x),(0≤x≤a , a为正常数)
(2)解:由(1)知y =28-( ![]() +x+3)
+x+3) ![]() ,
,
当且仅当 ![]() = x +3,即x =3时,上式取等号.
= x +3,即x =3时,上式取等号.
当a≥3时,促销费用投入3万元时,厂家的利润最大;
当0<a<3时,y在0≤x≤a上单调递增,
x = a , 函数有最大值.促销费用投入x = a万元时,厂家的利润最大.
综上述,当a≥3时,促销费用投入3万元时,厂家的利润最大;
当0<a<3时,促销费用投入x = a万元时,厂家的利润最大
【解析】(1)根据题目条件写出方程,进行化简即可,要注意自变量x的取值范围。
(2)先利用均值不等式求出最大值,再根据a的范围,判断投入多大时,利润最大。


科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,其中A(0,0),B(2,0),C(1,1),D(0,1),图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中
,其中 ![]() ,则
,则 ![]() 的取值范围是( )
的取值范围是( )
A.[2,3+ ![]() ]
]
B.[2,3+ ![]() ]
]
C.[3- ![]() , 3+
, 3+ ![]() ]
]
D.[3- ![]() , 3+
, 3+ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列{an}的前n项和Sn,且满足a3·a5=112,a1+a7=22.
(1)求等差数列{an}的第七项a7和通项公式an;
(2)若数列{bn}的通项bn=an+an+1,{bn}的前n项和Sn,写出使得Sn小于55时所有可能的bn的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,|an+1-an|=pn,n∈N*,Sn为数列{an}的前n项和.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若p=![]() ,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
(3)在(2)的条件下,令cn=n(an+1-an),求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A﹣EF﹣B大小为 ![]() .
.
(Ⅰ)求证:PQ∥平面BCD;
(Ⅱ)求二面角A﹣DB﹣E的余弦值.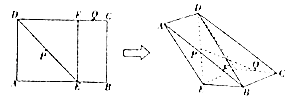
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的中心在原点焦点在
的中心在原点焦点在 ![]() 轴上,离心率等于
轴上,离心率等于 ![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 ![]() 的焦点.
的焦点.
(1)求椭圆 ![]() 的焦点;
的焦点;
(2)已知点 ![]() 在椭圆
在椭圆 ![]() 上,点
上,点 ![]() 是椭圆
是椭圆 ![]() 上不同于
上不同于 ![]() 的两个动点,且满足:
的两个动点,且满足: ![]() ,试问:直线
,试问:直线 ![]() 的斜率是否为定值?请说明理由.
的斜率是否为定值?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com