
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求实数![]() 及
及![]() 的值;
的值;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求
,求![]() 的取值范围并证明
的取值范围并证明![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,见解析.
,见解析.
【解析】
(1)根据导数的几何意义即可求出![]() ,再利用切点既在函数
,再利用切点既在函数![]() 图象上也在切线上,可得
图象上也在切线上,可得![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)![]() 有两个极值点
有两个极值点![]() ,
,![]() ,问题转化为
,问题转化为![]() ,即
,即![]() 有两个不相等的正实根,对
有两个不相等的正实根,对![]() 分为
分为![]() ,
,![]() 讨论,对
讨论,对![]() 时再结合判别式及对称轴再分为
时再结合判别式及对称轴再分为![]() 和
和![]() ,即可求出
,即可求出![]() 的取值范围;而
的取值范围;而![]() ,利用根与系数的关系求出
,利用根与系数的关系求出![]() ,
,![]() ,代入即可得到答案.
,代入即可得到答案.
(1)![]() ,由已知得
,由已知得![]() ,故
,故![]() ,所以
,所以![]() ,
,
![]() ,
,![]() ,解得
,解得![]() .
.
(2)由(1)可知![]() ,所以
,所以![]()
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,![]() 没有极值点,
没有极值点,
当![]() 时,令
时,令![]() ,其对称轴方程为
,其对称轴方程为![]() ,
,![]() ,
,
①若![]() 时,
时,![]() ,此时
,此时![]() 且不恒为零,
且不恒为零,
![]() 在
在![]() 上为减函数,
上为减函数,![]() 没有极值点.
没有极值点.
②若![]() 时,
时,![]() ,由
,由![]() ,即
,即![]() ,
,
则![]() 的两根为
的两根为![]() ,
,![]() 不妨设
不妨设![]() ,
,
由![]() ,
,![]() ,
,![]() ,故
,故![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
| 极大值 |
|
综上可知:求![]() 的取值范围是
的取值范围是![]() .
.
此时![]() ,
,![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,故
,故![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知方程![]() 表示的曲线为
表示的曲线为![]() 的图象,对于函数
的图象,对于函数![]() 有如下结论:①
有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 至少存在一个零点;③
至少存在一个零点;③![]() 的最大值为
的最大值为![]() ;④若函数
;④若函数![]() 和
和![]() 图象关于原点对称,则
图象关于原点对称,则![]() 由方程
由方程![]() 所确定;则正确命题序号为( )
所确定;则正确命题序号为( )
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn,满足:对任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求数列{an}的通项公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①在回归分析模型中,残差平方和越大,说明模型的拟合效果越好;
②某学校有男教师60名、女教师40名,为了解教师的体育爱好情况,在全体教师中抽取20名调查,则宜采用的抽样方法是分层抽样;
③线性相关系数![]() 越大,两个变量的线性相关性越弱;反之,线性相关性越强;
越大,两个变量的线性相关性越弱;反之,线性相关性越强;
④在回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 增加0.5个单位.
增加0.5个单位.
其中正确的结论是( )
A. ①②B. ①④
C. ②③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,AB=![]() ,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
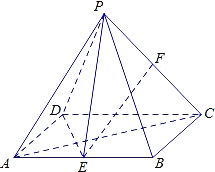
(1)求证:EF∥平面PAD;
(2)求证:平面PAC⊥平面PDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在区间
在区间![]() 上有两个极值点
上有两个极值点![]() ,且
,且![]() 恒成立,求满足条件的
恒成立,求满足条件的![]() 的最小值(极值点是指函数取极值时对应的自变量的值).
的最小值(极值点是指函数取极值时对应的自变量的值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情造成医用防护服紧缺,当地政府决定为防护服生产企业A公司扩大生产提供![]() (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到![]() (万件),其中k为工厂工人的复工率
(万件),其中k为工厂工人的复工率![]() ,A公司生产t万件防护服还需投入成本
,A公司生产t万件防护服还需投入成本![]() (万元).
(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的![]() (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com