
【题目】某工艺品厂要设计一个如图1所示的工艺品,现有某种型号的长方形材料如图2所示,其周长为4m,这种材料沿其对角线折叠后就出现图1的情况.如图,ABCD(AB>AD)为长方形的材料,沿AC折叠后AB'交DC于点P,设△ADP的面积为S2 , 折叠后重合部分△ACP的面积为S1 .
(Ⅰ)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(Ⅱ)求面积S2最大时,应怎样设计材料的长和宽?
(Ⅲ)求面积(S1+2S2)最大时,应怎样设计材料的长和宽?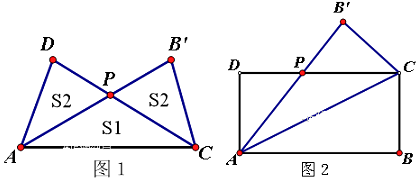
【答案】解:(Ⅰ)由题意,AB=x,BC=2﹣x,∵x>2﹣x,∴1<x<2
设DP=y,则PC=x﹣y,由△ADP≌△CB'P,故PA=PC=x﹣y,
由PA2=AD2+DP2,得(x﹣y)2=(2﹣x)2+y2
即: ![]() .
.
(Ⅱ)记△ADP的面积为S2,则 ![]() .
.
当且仅当 ![]() 时,S2取得最大值.
时,S2取得最大值.
故当材料长为 ![]() ,宽为
,宽为 ![]() 时,S2最大.
时,S2最大.
(Ⅲ) ![]()
于是令 ![]() ,∴
,∴ ![]()
∴关于x的函数 ![]() 在
在 ![]() 上递增,在
上递增,在 ![]() 上递减,
上递减,
∴当 ![]() 时,S1+2S2取得最大值.
时,S1+2S2取得最大值.
故当材料长为 ![]() ,宽为
,宽为 ![]() 时,S1+2S2最大
时,S1+2S2最大
【解析】(Ⅰ)设DP=y,根据图2将PC、AD用x,y表示,由图1可知![]() ,则PA=PC,在
,则PA=PC,在![]() 中,根据勾股定理列出等式;(Ⅱ)利用均值定理即可求解;(Ⅲ)构造函数F(t)=lnt-
中,根据勾股定理列出等式;(Ⅱ)利用均值定理即可求解;(Ⅲ)构造函数F(t)=lnt-![]() ,利用导数讨论函数F(t)的单调性.
,利用导数讨论函数F(t)的单调性.


科目:高中数学 来源: 题型:
【题目】已知F为抛物线C:x2=2py(p>0)的焦点,过F的直线l与C交于A,B两点,M为AB中点,点M到x轴的距离为d,|AB|=2d+1.
(1)求p的值;
(2)过A,B分别作C的两条切线l1 , l2 , l1∩l2=N.请选择x,y轴中的一条,比较M,N到该轴的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x的图象向左平移 ![]() 个单位后,得到函数y=g(x)的图象,下列关于y=g(x)的说法正确的是( )
个单位后,得到函数y=g(x)的图象,下列关于y=g(x)的说法正确的是( )
A.图象关于点(﹣ ![]() ,0)中心对称
,0)中心对称
B.图象关于x=﹣ ![]() 轴对称
轴对称
C.图象关于点(﹣ ![]() ,0)中心对称
,0)中心对称
D.图象关于x=﹣ ![]() 轴对称
轴对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为a1=2,且满足a1+a2+…+an﹣an+1=﹣2.
(I)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足 ![]() ,求数列{anbn}的前n项和Tn .
,求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将集合M={1,2,3,…15}表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为;请写出满足上述条件的集合M的5个三元子集 . (只写出一组)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1. 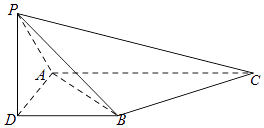
(Ⅰ)求证:AC∥平面PDB;
(Ⅱ)求二面角P﹣AB﹣C的余弦值;
(Ⅲ)线段PC上是否存在点E使得PC⊥平面ABE,如果存在,求 ![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣1+aex .
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)求f(x)的极值;
(3)当a=1时,曲线y=f(x)与直线y=kx﹣1没有公共点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PA=PC,底面ABC为正三角形.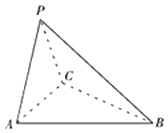
(Ⅰ)证明:AC⊥PB;
(Ⅱ)若平面PAC⊥平面ABC,AC=PC=2,求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com