
用0,1,2, 3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?
(1)156(2)216(3)270
解析试题分析:(1)符合要求的四位偶数可分为三类:
第一类:0在个位时有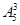 个;第二类:2或4在个位时,有
个;第二类:2或4在个位时,有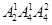 个;
个;
由分类加法计数原理知,共有四位偶数: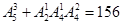 个. 4分
个. 4分
(2)五位数中5的倍数的数可分为两类:个位数上的数字是0的五位数有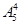 个;个位数上的数字是5的五位数有
个;个位数上的数字是5的五位数有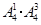 个.故所求五位数的个数共有
个.故所求五位数的个数共有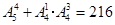 个. 8分
个. 8分
(3)符合要求的比1325大的四位数可分为三类:
第一类:形如2□□□,3□□□,4□□□,5□□□,共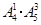 个;
个;
第二类:形如14□□,15□□,共有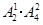 个;第三类:形如134□,135□,共有
个;第三类:形如134□,135□,共有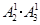 个;
个;
所以,无重复数字且比1325大的四位数共有: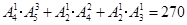 个. 13分
个. 13分
考点:排列问题
点评:本题中排数问题首先考虑特殊位置,如个位,最高位。在求解排列组合问题是当遇到特殊元素特殊位置的时候一般优先考虑,当元素相邻时采用捆绑法,当元素不相邻时采用插空法


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
4个男同学,3个女同学站成一排.
(1)男生甲必须排在正中间,有多少种不同的排法?
(2)3个女同学必须排在一起,有多少种不同的排法?
(3)任何两个女同学彼此不相邻,有多少种不同的排法?
(4)其中甲、乙两名同学之间必须有3人,有多少种不同的排法?
(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有4男3女共7位同学从前到后排成一列.
(1)有多少种不同方法?
(2)甲不站在排头,有多少种不同方法?
(3)三名女生互不相邻,有多少种不同方法?
(4)3名女生在队伍中按从前到后从高到矮顺序排列,有多少种不同方法?
(5)3名女生必须站在一起,有多少种不同方法?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有9本不同的书,分别求下列情况的不同分法的种数。
(1)分成三组,一组4本,一组3本,一组2本;
(2)分给三人,一人4本,一人3本,一人2本;
(3)平均分成三组。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com