
【题目】定义一:对于一个函数![]() ,若存在两条距离为
,若存在两条距离为![]() 的直线
的直线![]() 和
和![]() ,使得
,使得![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道.
的通道.
定义二:若一个函数![]() 对于任意给定的正数
对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,则称
的通道,则称![]() 在正无穷处有永恒通道.
在正无穷处有永恒通道.
下列函数①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中在正无穷处有永恒通道的函数序号是 .
. 其中在正无穷处有永恒通道的函数序号是 .
【答案】②③⑤
【解析】试题分析:①![]() ,随着
,随着![]() 的增大,函数值也在增大,无渐近线,故不存在一个实数
的增大,函数值也在增大,无渐近线,故不存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,故
的通道,故![]() 在正无穷处无永恒通道;②
在正无穷处无永恒通道;②![]() ,随着
,随着![]() 的增大,函数值趋近于
的增大,函数值趋近于![]() ,对于任意给定的正数
,对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,故
的通道,故![]() 在正无穷处有永恒通道;③
在正无穷处有永恒通道;③![]() ,随着
,随着![]() 的增大,函数值也在增大,有两条渐近线
的增大,函数值也在增大,有两条渐近线![]() ,对于任意给定的正数
,对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,故
的通道,故![]() 在正无穷处有永恒通道;④
在正无穷处有永恒通道;④![]() ,随着
,随着![]() 的增大,函数值也在增大,无渐近线,故不存在一个实数
的增大,函数值也在增大,无渐近线,故不存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为的通道,故
内有一个宽度为的通道,故![]() 在正无穷处无永恒通道;⑤
在正无穷处无永恒通道;⑤![]() ,随着
,随着![]() 的增大,函数值趋近于
的增大,函数值趋近于![]() ,趋近于
,趋近于![]() 轴,对于任意给定的正数
轴,对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,故
的通道,故![]() 在正无穷处有永恒通道.故答案为:②③⑤.
在正无穷处有永恒通道.故答案为:②③⑤.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为![]() (t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数,0).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,且AB的长度为2![]() ,求直线l的普通方程.
,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OB、CD是两条互相平行的笔直公路,且均与笔直公路OC垂直(公路宽度忽略不计),半径OC=1千米的扇形COA为该市某一景点区域,当地政府为缓解景点周边的交通压力,欲在圆弧AC上新增一个入口E(点E不与A、C重合),并在E点建一段与圆弧相切(E为切点)的笔直公路与OB、CD分别交于M、N.当公路建成后,计划将所围成的区域在景点之外的部分建成停车场(图中阴影部分),设∠CON=θ,停车场面积为S平方千米.
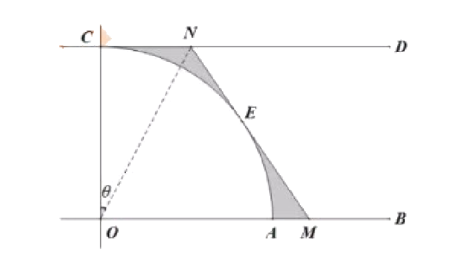
(1)求函数S=f(θ)的解析式,并写出函数的定义域;
(2)为对该计划进行可行性研究,需要预知所建停车场至少有多少面积,请计算当θ为何值时,S有最小值,并求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,圆
,圆![]() ,点
,点![]() 是圆上一动点,线段
是圆上一动点,线段![]() 的中垂线与线段
的中垂线与线段![]() 交于点
交于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且存在点
两点,且存在点![]() (其中
(其中![]() 不共线),使得
不共线),使得![]() 被
被![]() 轴平分,证明:直线
轴平分,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子里放有外形相同且编号为1,2,3,4,5的五个小球,其中1号与2号是黑球,3号、4号与5号是红球,从中有放回地每次取出1个球,共取两次.
(1)求取到的2个球中恰好有1个是黑球的概率;
(2)求取到的2个球中至少有1个是红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的![]() ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
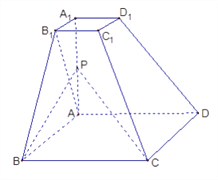
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
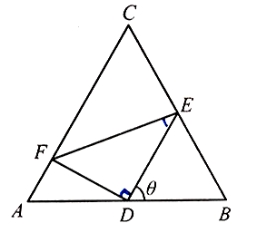
【题目】如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点,![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)求![]() 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com