
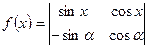 ,
,
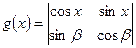 ,
, 是参数,
是参数,  ,
,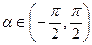 ,
,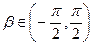
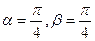 ,判别
,判别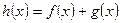 的奇偶性;
的奇偶性; 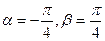 ,判别
,判别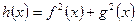 的奇偶性; (6分)
的奇偶性; (6分)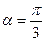 ,
,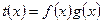 是偶函数,求
是偶函数,求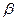 (4分)
(4分)
 推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题)
推广或是问题(2)的推广,问题(1)或(2)是问题(3)的特例。(不必证明命题) ,
,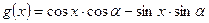 2分
2分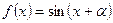 ,
, 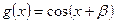
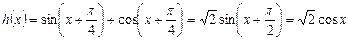 3分
3分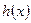 是偶函数
是偶函数 4分
4分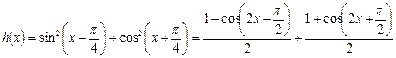
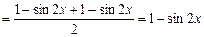 5分
5分 所以
所以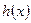 是非奇非偶函数
是非奇非偶函数  6分
6分 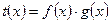 为偶函数,
为偶函数,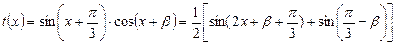 8分
8分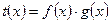 为
为 偶函数,所以
偶函数,所以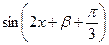 是偶函数, 9分
是偶函数, 9分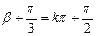 ,
,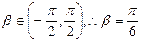 10分
10分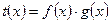 为偶函数
为偶函数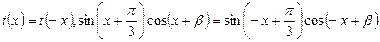
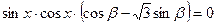 对一切
对一切 恒成立 8分
恒成立 8分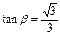 ,
, 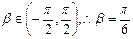 10分
10分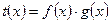 为偶函数
为偶函数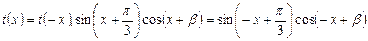
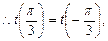
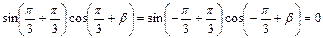 8分
8分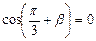 ,
, 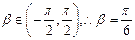 10分
10分 ,
,
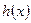 偶函数,
偶函数,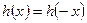 ,
,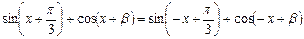
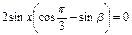 , 8分
, 8分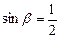 ,
, 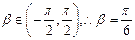 10分
10分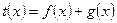 为偶函数
为偶函数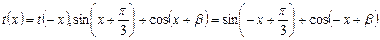
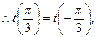 所以
所以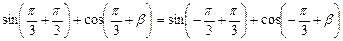 8分
8分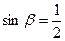 ,
, 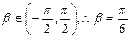 10分
10分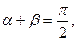
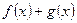 是偶函数;
是偶函数; 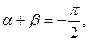
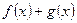 是奇函数;
是奇函数; 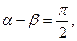
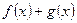 是非奇非偶函数;
是非奇非偶函数; 
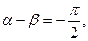
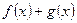 既奇又偶函数
既奇又偶函数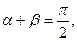
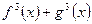 是偶函数 (数字不分奇偶)
是偶函数 (数字不分奇偶) 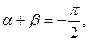
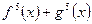 是奇函数
是奇函数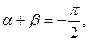
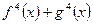 是偶函数
是偶函数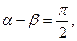
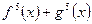 是非奇非偶函数 (数字不分奇偶,但需相同)
是非奇非偶函数 (数字不分奇偶,但需相同)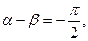
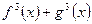 是既奇又偶函数 (数字只能奇数)
是既奇又偶函数 (数字只能奇数)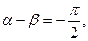

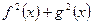 是非奇非偶函数
是非奇非偶函数 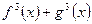 是偶函数 (数字不分奇偶,但相同), 则
是偶函数 (数字不分奇偶,但相同), 则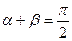
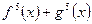 是奇函数 (数字只能正奇数) ,则
是奇函数 (数字只能正奇数) ,则 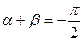
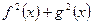 是偶函数 (数字只能正偶数), 则
是偶函数 (数字只能正偶数), 则 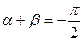
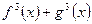 是偶函数 (数字只能正奇数),则
是偶函数 (数字只能正奇数),则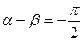
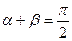 的充要条件是
的充要条件是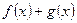 是偶函数
是偶函数 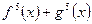 是奇函数 (数字只能正奇数) 的充要条件是
是奇函数 (数字只能正奇数) 的充要条件是 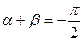
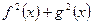 是偶函数 (数字只能正偶数)的充要条件是
是偶函数 (数字只能正偶数)的充要条件是 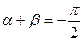
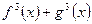 是偶函数 (数字只能正奇数)的充要条件是 则
是偶函数 (数字只能正奇数)的充要条件是 则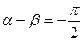
 逆命题,充要条件等均可以,限于篇幅省略) 18分
逆命题,充要条件等均可以,限于篇幅省略) 18分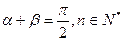 时,
时,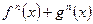 都是偶函数
都是偶函数 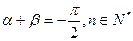 时,
时,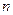 是正奇数,
是正奇数,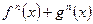 是奇函数
是奇函数 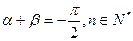 时,
时,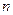 是正偶数,
是正偶数,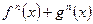 是偶函数
是偶函数 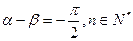 ,
,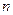 奇数,
奇数,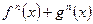 既奇又偶函数
既奇又偶函数 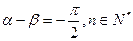 ,
,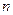 偶数,
偶数,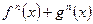 是非奇非偶函数
是非奇非偶函数 

科目:高中数学 来源:不详 题型:解答题

 ,其中
,其中 ,若点
,若点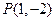 在矩阵
在矩阵 的变换下得到点
的变换下得到点 ,
, 的特征值及其对应的特征向量.
的特征值及其对应的特征向量. ,圆
,圆 的参数方程为
的参数方程为
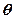 为参数).
为参数). 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵.
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵. 与曲线C2:
与曲线C2: (t∈R)交于A、B两点.求证:OA⊥OB.
(t∈R)交于A、B两点.求证:OA⊥OB. ,
, .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
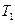 是逆时针旋转
是逆时针旋转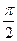 的旋转变换,对应的变换矩阵是
的旋转变换,对应的变换矩阵是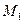 ;变换
;变换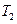 对应的变换矩阵是
对应的变换矩阵是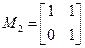 .
.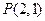 在变换
在变换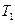 作用下的点
作用下的点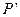 的坐标;
的坐标;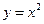 的图象依次在变换
的图象依次在变换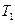 ,
,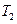 作用下所得曲线的方程.
作用下所得曲线的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com