
【题目】已知两点![]() 、
、![]() ,动点
,动点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 、
、![]() 的两个斜率存在,分别记为
的两个斜率存在,分别记为![]() 、
、![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹有两个交点
的轨迹有两个交点![]() 、
、![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知点![]() 在双曲线
在双曲线![]()
![]() (
(![]() ,
,![]() )上,且双曲线的一条渐近线的方程是
)上,且双曲线的一条渐近线的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两个不同的点,若以线段
两个不同的点,若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是一个菱形,三角形PAD是一个等腰三角形,∠BAD=∠PAD=![]() ,点E在线段PC上,且PE=3EC.
,点E在线段PC上,且PE=3EC.
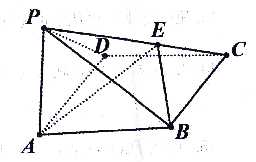
(1)求证:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )
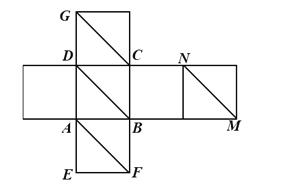
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴![]() 的交点为
的交点为![]() ,与
,与![]() 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,其中
,其中![]() 。由平面向量基本定理,对于平面内的向量
。由平面向量基本定理,对于平面内的向量![]() ,存在唯一有序实数对
,存在唯一有序实数对![]() ,使得
,使得![]() ,把
,把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标,也叫做向量
中的坐标,也叫做向量![]() 在斜坐标系
在斜坐标系![]() 中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如![]() 时,方程
时,方程![]() 表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
(1)若![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,求实数m的取值范围;
的夹角为锐角,求实数m的取值范围;
(2)若![]() ,已知点
,已知点![]() 和直线
和直线![]() ①求l的一个法向量;②求点A到直线l的距离。
①求l的一个法向量;②求点A到直线l的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来。某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图。
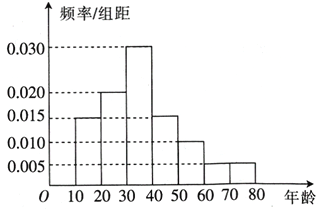
(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作,其中在卷五“三斜求积”中提出了已知三角形三边![]() 、
、![]() 、
、![]() ,求面积的公式,这与古希腊的海伦公式完全等价,其求法是“以小斜冥并大斜冥减中斜冥,余半之,自乘于上,以小斜冥乘大斜冥减上,余四约之,为实.一为从隅,开平方得积”若把以上这段文字写出公式,即若
,求面积的公式,这与古希腊的海伦公式完全等价,其求法是“以小斜冥并大斜冥减中斜冥,余半之,自乘于上,以小斜冥乘大斜冥减上,余四约之,为实.一为从隅,开平方得积”若把以上这段文字写出公式,即若![]() ,则
,则![]() .
.
(1)已知![]() 的三边
的三边![]() ,
,![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() 的面积
的面积![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com