
(2)在△ABC中,已知a=60,b=50,A=38°,求B(精确到1°)和c(保留两个有效数字).
思路分析:本题主要考查利用正弦定理解三角形问题.在△ABC中,已知两边和其中一边的对角,可运用正弦定理求解,但要注意解的个数的判定.
解:(1)由正弦定理及已知条件有![]() =
=![]() ,得sinA=
,得sinA=![]() .
.
∵a>b,∴A>B=45°.∴A=60°或120°.
当A=60°时,C=180°-45°-60°=75°,
c=![]() =
=![]() =
=![]() .
.
当A=120°时,C=180°-45°-120°=15°,
c=![]() =
=![]() =
=![]() .
.
综上,可知A=60°,C=75°,c=![]() 或A=120°,C=15°,c=
或A=120°,C=15°,c=![]() .
.
(2)∵b<a,∴B<A.∴B是锐角.
又∵sinB=![]() =
=![]() ≈0.513 1,∴B=31°.
≈0.513 1,∴B=31°.
∴C=180°-(A+B)≈180°-(38°+31°)=111°.
∴c=![]() ≈
≈![]() ≈91.
≈91.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
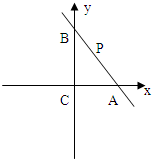 已知在△ABC中,∠ACB=90°,
已知在△ABC中,∠ACB=90°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com