
【题目】△ABC三个顶点坐标为A(0,1),B(0,﹣1),C(﹣2,1).
(I)求AC边中线所在直线方程;
(II)求△ABC的外接圆方程.
【答案】解:(I)般方程,代入 ![]() 三点坐标,解三元一次方程组,可得其外接圆的方程。
三点坐标,解三元一次方程组,可得其外接圆的方程。
(I)由于AC的中点为(﹣1,1),B(0,﹣1),
故AC边中线所在直线方程为2x+y+1=0.
(II)设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0,
则把A,B,C的坐标代入可得  ,
,
求得  ,故要求的圆的方程为 x2+y2+2x﹣1=0.
,故要求的圆的方程为 x2+y2+2x﹣1=0.
【解析】(1)求出中点坐标利用两点间的距离公式![]() 求出结果即可。(2)设出圆的一般方程把点的坐标代入得到关于D、E、F的方程组解出,进而得到圆的方程。
求出结果即可。(2)设出圆的一般方程把点的坐标代入得到关于D、E、F的方程组解出,进而得到圆的方程。
【考点精析】掌握圆的一般方程是解答本题的根本,需要知道圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.


科目:高中数学 来源: 题型:
【题目】如图,给出的是计算1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() 的值的一个程序框图,判断框内应填入的条件是( )
的值的一个程序框图,判断框内应填入的条件是( ) 
A.i<101?
B.i>101?
C.i≤101?
D.i≥101?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上. 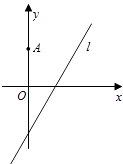
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,长方体 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 是棱
是棱 ![]() 上一点.
上一点.
(1)当点 ![]() 在
在 ![]() 上移动时,三棱锥
上移动时,三棱锥 ![]() 的体积是否变化?若变化,说明理由;若不变,求这个三棱锥的体积.
的体积是否变化?若变化,说明理由;若不变,求这个三棱锥的体积.
(2)当点 ![]() 在
在 ![]() 上移动时,是否始终有
上移动时,是否始终有 ![]() ,证明你的结论.
,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}是首项b1=1,b4=10的等差数列,设bn+2=3log ![]() an(n∈n*).
an(n∈n*).
(1)求证:{an}是等比数列;
(2)记cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)记dn=(3n+1)Sn , 若对任意正整数n,不等式 ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 恒成立,求整数m的最大值.
恒成立,求整数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,E,F分别是CD和BC的中点,若 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),则2x+y=;若
(x,y∈R),则2x+y=;若 ![]() =λ
=λ ![]() +μ
+μ ![]() (λ,μ∈R),则3λ+3μ= .
(λ,μ∈R),则3λ+3μ= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com