
分析 设f(x)=kx2-2x+6k,原问题等价于原问题等价于△≤0或$\left\{\begin{array}{l}{f(2)≥0}\\{f(3)≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$,由此求出k的取值范围
解答 解∵不等式对应的方程kx2-2x+6k=0的判别式为
△=4-24k2,
设f(x)=kx2-2x+6k,
则原问题等价于△≤0或$\left\{\begin{array}{l}{f(2)≥0}\\{f(3)≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$;
由△≤0,即4-24k2≤0,
解得k≤-$\frac{\sqrt{6}}{6}$或k≥$\frac{\sqrt{6}}{6}$,
又∵k>0,∴k≥$\frac{\sqrt{6}}{6}$;
由$\left\{\begin{array}{l}{f(2)≥0}\\{f(3)≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$,
即$\left\{\begin{array}{l}{10k-4≥0}\\{15k-6≥0}\\{2≤\frac{1}{k}≤3}\end{array}\right.$,
解得$\frac{2}{5}$≤k≤$\frac{1}{2}$;
综上,符合条件的k的取值范围是[$\frac{2}{5}$,+∞).
点评 本题考查了含有字母系数的不等式的解法与应用问题,也考查了不等式的恒成立问题,解题时应对字母系数进行分析、讨论,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
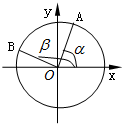 如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.
如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com