��֪ԲC����x-3��2+��y-4��2=4��ֱ��l��x+2y+2=0��ֱ��m����ԲC�ⶨ��A��1��0����
��1����m��ԲC�ཻ��P��Q���㣬�ʣ���Բ��C��ֱ��m����ȡ��ֵʱ��������CPQ�����ȡ���ֵ����д����ʱm��ֱ�߷��̣�
��2����ֱ��m��ԲC�ཻ��P��Q���㣬��l����N�㣬���߶�PQ���е�ΪM�����ж�|AM|•|AN|�Ƿ�Ϊ��ֵ�����������ֵ��������˵�����ɣ�
��������1��ֱ����Բ�ཻ��б�ʱض����ڣ��Ҳ�Ϊ0����ֱ�߷���Ϊkx-y-k=0����Բ�ĵ�ֱ�ߵľ���Ϊd������������CPQ�����s����d�ĺ�����ϵʽ����������ֵ�������õ㵽ֱ�ߵľ��빫ʽ�з��̼��ɵý�
��2��ֱ����Բ�ཻ��б�ʱض����ڣ��Ҳ�Ϊ0����ֱ�߷���Ϊkx-y-k=0��������ֱ����ֱ��l������������õ�N�����꣬�ٽ�ֱ����Բ�ķ�������������Τ�ﶨ�������M������꣬��A��1��0�������������ľ��빫ʽ���㲢����õ���|AM|•|AN|�Ĵ���ʽ���ɵý�
����⣺��1��ֱ����Բ�ཻ��б�ʱض����ڣ��Ҳ�Ϊ0����ֱ�߷���Ϊkx-y-k=0��
��Բ�ĵ�ֱ�ߵľ���Ϊd�֡�������CPQ���
�൱d=
ʱ��Sȡ�����ֵ2��
d==��k=1��k=7��ֱ�߷���Ϊy=x-1����y=7x-7
��2���⣺ֱ����Բ�ཻ��б�ʱض����ڣ��Ҳ�Ϊ0��
����ֱ�߷���Ϊkx-y-k=0
��
��
N(��-)����
�ã�1+k
2��x
2-��2k
2+8k+6��x+k
2+8k+21=0��
��
x^+x^=��
M(��)��
|AM|•|AN|=•=
•=6Ϊ��ֵ
���������⿼����ֱ����Բ��λ�ù�ϵ���㵽ֱ�ߵľ��빫ʽ������֮��ľ��빫ʽ���ص㿼���˶�����Τ�ﶨ�����������Ľ��ⷽ�������գ�����ʱҪ������ᣬ�������



 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
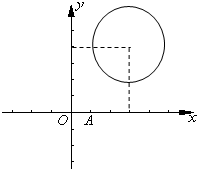 ��֪ԲC����x-3��2+��y-4��2=4��
��֪ԲC����x-3��2+��y-4��2=4��