
分析 利用周期与对称性得出f(x)的函数图象,根据交点个数列出不等式得出k的范围.
解答 解:∵当x>2时,f(x)=f(x-1),
∴f(x)在(1,+∞)上是周期为1的函数,
作出y=f(x)的函数图象如下: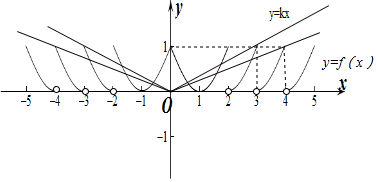
∵方程f(x)=kx恰有3个不同的根,
∴y=f(x)与y=kx有三个交点,
若k>0,则$\left\{\begin{array}{l}{3k≤1}\\{4k>1}\end{array}\right.$,解得$\frac{1}{4}$<k≤$\frac{1}{3}$,
若k<0,由对称性可知-$\frac{1}{3}$≤k<-$\frac{1}{4}$.
故答案为:[-$\frac{1}{3}$,-$\frac{1}{4}$)∪($\frac{1}{4}$,$\frac{1}{3}$].
点评 本题考查了函数零点与函数图象的关系,函数周期与奇偶性的应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:解答题
已知f(x)=3x2-2x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设bn=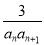 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<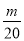 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
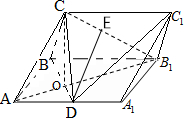 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )
元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com