
【题目】已知函数 ![]() .
.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)将函数y=sin2x的图象向左平移 ![]() 个单位,向下平移b个单位,得到函数y=f(x)的图象,求ab的值;
个单位,向下平移b个单位,得到函数y=f(x)的图象,求ab的值;
(Ⅲ)求函数f(x)在 ![]() 上的值域.
上的值域.
【答案】解:(I) ![]()
= ![]()
= ![]()
= ![]() .
.
函数f(x)的最小正周期是 ![]() ;
;
(II)由(I)得, ![]() ,
,
可知 ![]() ,
, ![]() .则
.则 ![]() .
.
(Ⅲ)∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
∴f(x)的值域为 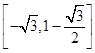
【解析】(I)先根据三角函数的二倍角公式和两角和与差的正弦公式将函数化简为y=Asin(wx+φ)的形式,根据T= ![]() 可得答案.(II)将y=sin2x进行平移可得sin2(x+a)﹣b,然后令
可得答案.(II)将y=sin2x进行平移可得sin2(x+a)﹣b,然后令 ![]() 可解出a,b的值.(Ⅲ)先根据x的范围求出2x+
可解出a,b的值.(Ⅲ)先根据x的范围求出2x+ ![]() 的范围,再由三角函数的性质可得到答案.
的范围,再由三角函数的性质可得到答案.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两地相距500千米,一辆货车从甲地行驶到乙地,规定速度不得超过100千米![]() 小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (千米
(千米![]() 时)的平方成正比,比例系数为0.01;固定部分为
时)的平方成正比,比例系数为0.01;固定部分为![]() 元(
元(![]() ).
).
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米
(千米![]() 时)的函数,并指出这个函数的定义域;
时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,直线l:
,直线l:![]() (其中
(其中![]() ).
).
(Ⅰ)求直线l所经过的定点P的坐标;
(Ⅱ)若分别过A,B且斜率为![]() 的两条平行直线截直线l所得线段的长为
的两条平行直线截直线l所得线段的长为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图像如图所示,
的部分图像如图所示,![]() 分别是图像的最低点和最高点,
分别是图像的最低点和最高点,![]()

(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再把所得图像上各点横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,再把所得图像上各点横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知两条公路![]() 的交汇点
的交汇点![]() 处有一学校,现拟在两条公路之间的区域内建一工厂
处有一学校,现拟在两条公路之间的区域内建一工厂![]() ,在两公路旁
,在两公路旁![]() (异于点
(异于点![]() )处设两个销售点,且满足
)处设两个销售点,且满足![]() ,
,![]() (千米),
(千米),![]() (千米),设
(千米),设![]() .
.

(1)试用![]() 表示
表示![]() ,并写出
,并写出![]() 的范围;
的范围;
(2)当![]() 为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最远).
为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最远).
(注:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx﹣x+a+1
(1)若存在 x∈(0,+∞)使得f(x)≥0成立,求a的范围;
(2)求证:当x>1时,在(1)的条件下, ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会于2017年10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚“情况,从某县调查得到农村居民2011年至2017年家庭人均纯收入![]() (单位:百元)的数据如下表:
(单位:百元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入能否达到“全面建成小康社会”的标准?
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
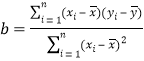 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com