
分析 分两类求解:①水平渐近线,②垂直渐近线,都是通过取极限的方式确定其方程.
解答 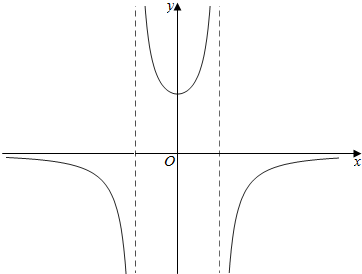 解:函数f(x)图象的渐近线有两类:
解:函数f(x)图象的渐近线有两类:
①水平渐近线,
$\underset{lim}{x→+∞}$f(x)=$\underset{lim}{x→+∞}$$\frac{4}{2-{x}^{2}}$=0,
$\underset{lim}{x→-∞}$f(x)=$\underset{lim}{x→+∞}$$\frac{4}{2-{x}^{2}}$=0,
由此可知,y=0为该函数图象的渐近线;
②垂直渐近线,
令2-x2=0解得,x=$\sqrt{2}$或x=-$\sqrt{2}$,
即$\underset{lim}{x→\sqrt{2}}$f(x)=∞,$\underset{lim}{x→-\sqrt{2}}$f(x)=∞,
综合得,该函数有三条渐近线,方程分别为:
y=0,x=-$\sqrt{2}$,x=$\sqrt{2}$(如右图).
点评 本题主要考查了函数的图象和性质,涉及函数图象的渐近线的求法,属于基础题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 10 | 70 |
| 北方学生 | 20 | 10 | 30 |
| 合计 | 80 | 20 | 100 |
| P(K2≥K) | 0.100 | 0.050 | 0.010 |
| K | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=3 | B. | y=2 | C. | y=$\frac{3}{2}$x | D. | y=$\frac{2}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com