
【题目】已知![]() ,
, ![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)求出![]() ,利用导数与单调性的关系,分类求解;(2))由已知,
,利用导数与单调性的关系,分类求解;(2))由已知, ![]() ,分离参数,则
,分离参数,则![]() ,构造
,构造![]() (x>0) 通过研究h(x)的最值确定a的范围.
(x>0) 通过研究h(x)的最值确定a的范围.
试题解析:解:(1)![]() ,
,
当![]() ,
, ![]() ,f(x)单调递减,当
,f(x)单调递减,当![]() ,
, ![]() ,f(x)单调递增
,f(x)单调递增
①![]() ,没有最小值;
,没有最小值;
②![]() ,即
,即![]() 时,
时, ![]() ;
;
③![]() ,即
,即![]() 时,f(x)在[t,t+2]上单调递增,
时,f(x)在[t,t+2]上单调递增, ![]() ;
;
所以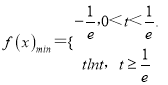 ;
;
(2)由已知, ![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
①x∈(0,1),h'(x)<0,h(x)单调递减,
②x∈(1,+∞),h'(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
所以a≤h(x)min=4;,所以a的范围是(-∞,4].


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(1)证明方程f(x)=g(x)在区间(1,2)内有且仅有唯一实根;
(2)记max{a,b}表示a,b两个数中的较大者,方程f(x)=g(x)在区间(1,2)内的实数根为x0 , m(x)=max{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)内有两个不等的实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|.
(1)当a=2时,解不等式f(x)≥7﹣|x﹣1|;
(2)若f(x)≤1的解集为[0,2], ![]() =a(m>0,n>0),求证:m+4n≥2
=a(m>0,n>0),求证:m+4n≥2 ![]() +3.
+3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1
①若函数G(x)有两相异零点且![]() 在
在![]() 上是减函数,求实数m的取值范围。
上是减函数,求实数m的取值范围。
②是否存在整数a,b使得![]() 的解集恰好为
的解集恰好为![]() 若存在,求出a,b的值,若不存在,请说明理由。
若存在,求出a,b的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为{x|x≠0}的函数f(x)满足:f(xy)=f(x)f(y),f(x)>0且在区间(0,+∞)上单调递增,若m满足f(log3m)+f( ![]() )≤2f(1),则实数m的取值范围是( )
)≤2f(1),则实数m的取值范围是( )
A.[ ![]() ,1)∪(1,3]
,1)∪(1,3]
B.[0, ![]() )∪(1,3]
)∪(1,3]
C.(0, ![]() ]
]
D.[1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com