
【题目】设函数![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)如果![]() 且关于
且关于![]() 的方程
的方程![]() 有两解
有两解![]() ,
, ![]() (
(![]() ),证明
),证明![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
(1)求解函数的导函数,分类讨论可得:
①若![]() ,则当
,则当![]() 时,数
时,数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() 函数
函数![]() 单调递增;
单调递增;
②若![]() ,函数
,函数![]() 单调递增;
单调递增;
③若![]() ,则当
,则当![]() 时,函数
时,函数![]() 单调递减,当
单调递减,当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
(2)原问题即证明![]() ,构造新函数
,构造新函数![]()
![]() ,结合新函数的性质和题意即可证得结论.
,结合新函数的性质和题意即可证得结论.
试题解析:
(1)由![]() ,可知
,可知![]()
![]() .
.
因为函数![]() 的定义域为
的定义域为![]() ,所以,
,所以,
①若![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增;
单调递增;
②若![]() ,则当
,则当![]() 在
在![]() 内恒成立,函数
内恒成立,函数![]() 单调递增;
单调递增;
③若![]() ,则当
,则当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
(2)要证![]() ,只需证
,只需证![]() .
.
设![]()
![]() ,
,
因为![]() ,
,
所以![]() 为单调递增函数.
为单调递增函数.
所以只需证![]() ,
,
即证![]() ,
,
只需证![]()
![]() .(*)
.(*)
又![]() ,
, ![]() ,
,
所以两式相减,并整理,得![]()
![]() .
.
把![]()
![]() 代入(*)式,
代入(*)式,
得只需证![]() ,
,
可化为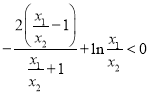 .
.
令![]() ,得只需证
,得只需证![]() .
.
令![]() (
(![]() ),
),
则![]()
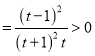 ,
,
所以![]() 在其定义域上为增函数,
在其定义域上为增函数,
所以![]() .
.
综上得原不等式成立.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足3an﹣2Sn﹣1=0.
(1)求数列{an}的通项公式;
(2)bn= ![]() ,数列{bn}的前n项和为Tn , 求f(n)=
,数列{bn}的前n项和为Tn , 求f(n)= ![]() (n∈N+)的最大值.
(n∈N+)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有大型超市200家、中型超市400家、小型超市1400 家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A.70家
B.50家
C.20家
D.10家
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( ) 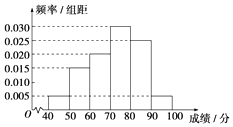
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥ABC﹣A1B1C1中,底面ABC是边长为2的正三角形,侧棱AA1⊥底面ABC,AA1= ![]() ,P、Q分别是AB、AC上的点,且PQ∥BC.
,P、Q分别是AB、AC上的点,且PQ∥BC. 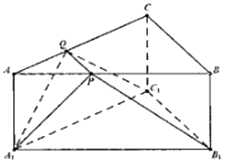
(1)若平面A1PQ与平面A1B1C1相交于直线l,求证:l∥B1C1;
(2)当平面A1PQ⊥平面PQC1B1时,确定点P的位置并说明理由.S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com