
【题目】设a是从集合{1,2,3,4}中随机取出的一个数,b是从集合{1,2,3}中随机取出的一个数,构成一个基本事件(a,b)。记“在这些基本事件中,满足logba≥1为事件A,则A发生的概率是 .
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
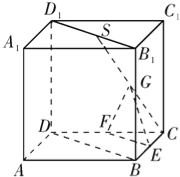
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的参数方程为: ![]() (φ为参数),直线l的极坐标方程为ρ(cosθ+sinθ)=4.
(φ为参数),直线l的极坐标方程为ρ(cosθ+sinθ)=4.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若点P在曲线C上,点Q在直线l上,求线段PQ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的函数f(x)=a(x+ ![]() )﹣|x﹣
)﹣|x﹣ ![]() |(a∈R).
|(a∈R).
(1)当a= ![]() 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(2)若f(x)≥ ![]() x对任意的x>0恒成立,求a的取值范围.
x对任意的x>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内圆心为![]() 的圆的方程为
的圆的方程为![]() ,点
,点![]() 是圆上的动点,点
是圆上的动点,点![]() 是平面内任意一点,若线段
是平面内任意一点,若线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,则点
,则点![]() 的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有两个关于“袋子中装有红、白两种颜色的相同小球,从袋中无放回地取球”的游戏规则,这两个游戏规则公平吗?为什么?
游 戏 1 | 游 戏 2 |
2个红球和2个白球 | 3个红球和1个白球 |
取1个球,再取1个球 | 取1个球,再取1个球 |
取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的![]() 倍和
倍和![]() 倍后,得到曲线
倍后,得到曲线![]()
(1)试写出曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求点
上求点![]() ,使得点
,使得点![]() 到直线
到直线![]() 的距离最大,并求距离最大值.
的距离最大,并求距离最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
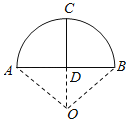
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com