
【题目】某商场经营某种商品,在某周内获纯利![]() (元)与该周每天销售这种商品数
(元)与该周每天销售这种商品数![]() 之间的一组数据关系如表:
之间的一组数据关系如表:
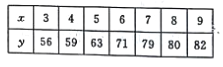
(I)画出散点图;
(II)求纯利![]() 与每天销售件数
与每天销售件数![]() 之间的回归直线方程;
之间的回归直线方程;
(III)估计当每天销售的件数为12件时,每周内获得的纯利为多少?
附注:
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的两个焦点分别为
的两个焦点分别为 ![]() ,
, ![]() ,且经过点
,且经过点 ![]() .
.
(Ⅰ)求椭圆 ![]() 的标准方程;
的标准方程;
(Ⅱ) ![]() 的顶点都在椭圆
的顶点都在椭圆 ![]() 上,其中
上,其中 ![]() 关于原点对称,试问
关于原点对称,试问 ![]() 能否为正三角形?并说明理由.
能否为正三角形?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() …,
…,![]() …,
…,![]() ,对于
,对于![]() …,
…,![]() ,B=(
,B=(![]() …,
…,![]() ,定义A与B的差为
,定义A与B的差为
![]() …
…![]() ,A与B之间的距离为
,A与B之间的距离为![]() .
.
(Ⅰ)若![]() ,求
,求![]() ;
;
(Ⅱ)证明:对任意![]() ,有
,有
(i)![]() ,且
,且![]() ;
;
(ii)![]() 三个数中至少有一个是偶数;
三个数中至少有一个是偶数;
(Ⅲ)对于![]() …
…![]() …
…![]() ,再定义一种A与B之间的运算,并写出两条该运算满足的性质(不需证明).
,再定义一种A与B之间的运算,并写出两条该运算满足的性质(不需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,若对任意
中,若对任意![]() 都有
都有![]() (
(![]() 为常数)成立,则称
为常数)成立,则称![]() 为“等差比数列”,下面对“等差比数列” 的判断:①
为“等差比数列”,下面对“等差比数列” 的判断:①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为
;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为![]() (其中
(其中![]() ,且
,且![]() ,
,![]() )的数列一定是等差比数列,其中正确的判断是( )
)的数列一定是等差比数列,其中正确的判断是( )
A. ①③④ B. ②③④ C. ①④ D. ①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P(x,y)(其中y ![]() )到x轴的距离比它到点F(0,1)的距离少1.
)到x轴的距离比它到点F(0,1)的距离少1.
(1)求动点P的轨迹方程;
(2)若直线l:x-y+1=0与动点P的轨迹交于A、B两点,求△OAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列{an}的前n项和Sn,且满足a3·a5=112,a1+a7=22.
(1)求等差数列{an}的第七项a7和通项公式an;
(2)若数列{bn}的通项bn=an+an+1,{bn}的前n项和Sn,写出使得Sn小于55时所有可能的bn的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列 ![]() 中,
中, ![]() ,其前
,其前 ![]() 项和为
项和为 ![]() ,等比数列
,等比数列 ![]() 的各项均为正数,
的各项均为正数, ![]() ,公比为
,公比为 ![]() ,且
,且 ![]() ,
, ![]() .
.
(Ⅰ)求 ![]() 与
与 ![]() .
.
(Ⅱ)设数列 ![]() 满足
满足 ![]() ,求
,求 ![]() 的前
的前 ![]() 项和
项和 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com