Question

【题目】在无穷数列{an}中，a1=p是正整数，且满足 （Ⅰ）当a3=9时，给出p的值；（结论不要求证明）
（Ⅱ）设p=7，数列{an}的前n项和为Sn ， 求S150；
（Ⅲ）如果存在m∈N* ， 使得am=1，求出符合条件的p的所有值．

Answer 1

【答案】解：（Ⅰ）p=36，或13．

（Ⅱ）由题意，a1=7，

代入，得a2=12，a3=6，a4=3，a5=8，a6=4，a7=2，a8=1，a9=6，…

所以数列{an}中的项，从第三项起每隔6项重复一次（注：a3=a9），

故S150=a1+a2+24（a3+a4+…+a8）+a3+a4+a5+a6

=7+12+24（6+3+8+4+2+1）+6+3+8+4=616．

（Ⅲ）由数列{an}的定义，知 ．

设t为数列{an}中最小的数，即 ，

又因为当an为偶数时， ，

所以t必为奇数．

设ak=t，则ak+1=t+5， ，

所以 ，解得t≤5．

所以t∈{1，3，5}．

如果ak=t=3，

那么由数列{an}的定义，得ak+1=8，ak+2=4，ak+3=2，ak+4=1，

这显然与t=3为{an}中最小的数矛盾，

所以t≠3．

如果ak=t=5，

当k=1时，p=5；

当k≥2时，由数列{an}的定义，得ak﹣1能被5整除，…，得a1=p被5整除；

所以当且仅当 时，t=5．

这与题意不符．

所以当 时，数列{an}中最小的数t=1，

即符合条件的p值的集合是{r|r∈N*，且r不能被5整除}．

【解析】（Ⅰ）由分段数列，推断计算即可得到所求p的值；（Ⅱ）由题意可得数列{an}中的项，从第三项起每隔6项重复一次，即可得到所求和；（Ⅲ）由数列{an}的定义，知 ．设t为数列{an}中最小的数，即 ，推得t∈{1，3，5}．分别讨论t=3，5，1，推理，即可得到符合条件的p值的集合．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系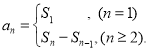；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．