
【题目】袋中装有9个形状大小相同但颜色不同的小球,其中红色、蓝色、黄色球各3个,现从中随机地连取3次球,每次取1个,记事件A为“3个球都是红球”,事件B为“3 个球颜色不全相同” (Ⅰ)若每次取后不放回,分别求出事件A和事件B的概率(用数字作答);
(Ⅱ)若每次取后放回,分别求出事件A和事件B的概率(用数字作答).
【答案】解:(Ⅰ)袋中装有9个形状大小相同但颜色不同的小球,其中红色、蓝色、黄色球各3个,
现从中随机地连取3次球,每次取1个,记事件A为“3个球都是红球”,事件B为“3 个球颜色不全相同”
每次取后不放回,基本事件总数n=9×8×7=504,
事件A包含的基本事件个数mA=3×2×1=6,
事件B的对立事件是“3个球颜色全相同”,
∴事件A的概率p(A)= ![]() =
= ![]() =
= ![]() .
.
事件B的概率p(B)=1﹣ ![]() =
= ![]() .
.
(Ⅱ)每次取后放回,基本事件总数n′=9×9×9=729,
事件A包含的基本事件个数mA′=3×3×3=27,
事件B的对立事件是“3个球颜色全相同”,
∴事件A的概率p(A)= ![]() =
= ![]() =
= ![]() .
.
事件B的概率p(B)=1﹣ ![]() =
= ![]()
【解析】(Ⅰ)每次取后不放回,基本事件总数n=9×8×7=504,事件A包含的基本事件个数mA=3×2×1=6,事件B的对立事件是“3个球颜色全相同”,由此利用等可能事件概率计算公式能求出事件A的概率,利用对立事件概率计算公式能求出事件B的概率.(Ⅱ)每次取后放回,基本事件总数n′=9×9×9=729,事件A包含的基本事件个数mA′=3×3×3=27,事件B的对立事件是“3个球颜色全相同”,由此利用等可能事件概率计算公式能求出事件A的概率,利用对立事件概率计算公式能求出事件B的概率.


科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 上的点
上的点 ![]() 到焦点
到焦点 ![]() 的距离为
的距离为 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
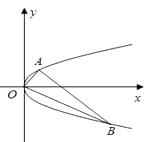
(2)设 ![]() ,
, ![]() 是抛物线上分别位于
是抛物线上分别位于 ![]() 轴两侧的两个动点,且
轴两侧的两个动点,且 ![]() (其中
(其中 ![]() 为坐标原点).求证:直线
为坐标原点).求证:直线 ![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2﹣3x,函数g(x)的图象在点(1,g(x))处的切线平行于x轴.
(1)求a的值;
(2)求函数g(x)的极小值;
(3)设斜率为k的直线与函数f(x)的图象交于两点A(x1 , y1),B(x2 , y2),(x1<x2),证明: ![]() <k<
<k< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的方差为( )
A.![]()
B.![]()
C.36
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com