若函数f(x)满足f(x)=cosx(x∈R),则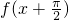 =
=
- A.
sinx
- B.
-sinx
- C.
cosx
- D.
-cosx
B
分析:根据f(x)=cosx(x∈R),可得
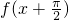
=cosx

,利用诱导公式化为-sinx.
解答:∵f(x)=cosx(x∈R),∴
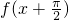
=cosx

=-sinx,
故选B.
点评:本题考查利用诱导公式进行化简求值,属于容易题.
练习册系列答案
相关习题
科目:高中数学
来源:2012-2013学年湖北省荆州中学高三(上)第一次质量检测数学试卷 (理科)(解析版)
题型:选择题
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),则x>2时,f(x)单调递增,若x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)与0的大小关系是( )
A.f(x1)+f(x2)>0
B.f(x1)+f(x2)=0
C.f(x1)+f(x2)<0
D.f(x1)+f(x2)≤0
查看答案和解析>>
科目:高中数学
来源:2012-2013学年河南省洛阳一中高三(上)期中数学考前选择题强化训练(解析版)
题型:选择题
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),则x>2时,f(x)单调递增,若x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)与0的大小关系是( )
A.f(x1)+f(x2)>0
B.f(x1)+f(x2)=0
C.f(x1)+f(x2)<0
D.f(x1)+f(x2)≤0
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖北省荆州中学高三(上)第一次质量检测数学试卷 (文科)(解析版)
题型:选择题
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),则x>2时,f(x)单调递增,若x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)与0的大小关系是( )
A.f(x1)+f(x2)>0
B.f(x1)+f(x2)=0
C.f(x1)+f(x2)<0
D.f(x1)+f(x2)≤0
查看答案和解析>>
科目:高中数学
来源:2011-2012学年湖南省湘西州边城高级中学高三(上)月考数学试卷(解析版)
题型:选择题
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),则x>2时,f(x)单调递增,若x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)与0的大小关系是( )
A.f(x1)+f(x2)>0
B.f(x1)+f(x2)=0
C.f(x1)+f(x2)<0
D.f(x1)+f(x2)≤0
查看答案和解析>>
科目:高中数学
来源:2010-2011学年湖南省湘西州古丈县补习学校高三(上)第一次月考数学试卷(理科)(解析版)
题型:选择题
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),则x>2时,f(x)单调递增,若x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)与0的大小关系是( )
A.f(x1)+f(x2)>0
B.f(x1)+f(x2)=0
C.f(x1)+f(x2)<0
D.f(x1)+f(x2)≤0
查看答案和解析>>

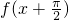 =
= 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案