
分析 (1)求出导数,利用f'(1)=-1,求解即可.
(2)设g(x)=lnx-x,则$g'(x)=\frac{1}{x}-1$,判断函数的单调性,求出最值即可得到结果.
解答 解:(1)对f(x)求导,得f'(x)=1+lnx+2ax,
所以f'(1)=1+2a=-1,解得a=-1.
(2)由f(x)-mx≤-1,得xlnx-x2-mx≤0,
因为x∈(0,+∞),所以对于任意x∈(0,+∞),都有lnx-x≤m.
设g(x)=lnx-x,则$g'(x)=\frac{1}{x}-1$,
令g'(x)=0,解得x=1,
当x变化时,g(x)与g'(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| g'(x) | + | 0 | - |
| g(x) | 增 | 极大值 | 减 |
点评 本题考查函数的导数的应用,函数的最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 2-2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{2}$-1 | D. | 1-$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
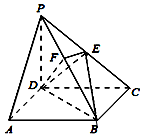 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,EF⊥PB交PB于点F.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,EF⊥PB交PB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com