
【题目】如图是正四面体的平面展开图,![]() 分别是
分别是![]() 的中点,在这个正四面体中:①
的中点,在这个正四面体中:①![]() 与
与![]() 平行;②
平行;②![]() 与
与![]() 为异面直线;③
为异面直线;③![]() 与
与![]() 成60°角;④
成60°角;④![]() 与
与![]() 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析:正四面体的平面展开图复原为正四面体A(B、C)﹣DEF,
①,依题意,MN∥AF,而DE与AF异面,从而可判断DE与MN不平行;
②,假设BD与MN共面,可得A、D、E、F四点共面,导出矛盾,从而可否定假设,肯定BD与MN为异面直线;
③,依题意知,GH∥AD,MN∥AF,∠DAF=60°,于是可判断GH与MN成60°角;
④,连接GF,那么A点在平面DEF的射影肯定在GF上,通过线面垂直得到线线垂直.
详解:将正四面体的平面展开图复原为正四面体A(B、C)﹣DEF,如图:
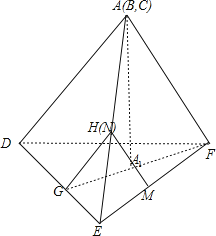
对于①,M、N分别为EF、AE的中点,则MN∥AF,而DE与AF异面,故DE与MN不平行,故①错误;
对于②,BD与MN为异面直线,正确(假设BD与MN共面,则A、D、E、F四点共面,与ADEF为正四面体矛盾,故假设不成立,故BD与MN异面);
对于③,依题意,GH∥AD,MN∥AF,∠DAF=60°,故GH与MN成60°角,故③正确;
对于④,连接GF,A点在平面DEF的射影A1在GF上,∴DE⊥平面AGF,DE⊥AF,
而AF∥MN,∴DE与MN垂直,故④正确.
综上所述,正确命题的序号是②③④,
故答案为:②③④.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】已知下面四个命题:
①“若![]() ,则
,则![]() 或
或![]() ”的逆否命题为“若
”的逆否命题为“若![]() 且
且![]() ,则
,则![]() ”
”
②“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
③命题![]() 存在
存在![]() ,使得
,使得![]() ,则
,则![]() :任意
:任意![]() ,都有
,都有![]()
④若![]() 且
且![]() 为假命题,则
为假命题,则![]() 均为假命题,其中真命题个数为( )
均为假命题,其中真命题个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=![]() (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为![]() ,弦长为
,弦长为![]() 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中![]() ,
,![]() )
)
A. 15 B. 16 C. 17 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车制造商在2019年年初公告:公司计划2019年的生产目标为43万辆.已知该公司近三年的汽车生产量如表所示:
年份(年) | 2016 | 2017 | 2018 |
产量(万辆) | 8 | 18 | 30 |
如果我们分别将2016,2017,2018,2019定义为第一、二、三、四年.现在有两个函数模型:二次函数模型![]() ,指数型函数模型
,指数型函数模型![]() ,哪个模型能更好地反映该公司年产量y与年份x的关系?
,哪个模型能更好地反映该公司年产量y与年份x的关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数![]() 的基本性质:定义域,奇偶性,单调性,值域(结论不需证明),并作出函数
的基本性质:定义域,奇偶性,单调性,值域(结论不需证明),并作出函数![]() 的图象;
的图象;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 恰有
恰有![]() 个不同的实数解,求实数
个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三个数![]() 成等差数列,记
成等差数列,记![]() 对应点的曲线是
对应点的曲线是![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,点
,点![]() ,点
,点![]() ,过点
,过点![]() 任作直线
任作直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() ,求
,求![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,动点P,Q从点
中,动点P,Q从点![]() 出发在单位圆上运动,点P按逆时针方向每秒钟转
出发在单位圆上运动,点P按逆时针方向每秒钟转![]() 弧度,点Q按顺时针方向每秒钟转
弧度,点Q按顺时针方向每秒钟转![]() 弧度,则P,Q两点在第2019次相遇时,点P的坐标为________.
弧度,则P,Q两点在第2019次相遇时,点P的坐标为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com