
某旅游公司提供甲、乙、丙三处旅游景点,游客选择游玩哪个景点互不影响,已知某游客选择游甲地而不选择游乙地和丙地的概率为0.08,选择游甲地和乙地而不选择游丙地的概率为0.12,在甲、乙、丙三处旅游景点中至少选择游一个景点0.88,用表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
(Ⅰ)记“函数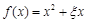 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率;
(Ⅱ)求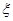 的概率分布列及数学期望.
的概率分布列及数学期望.
(Ⅰ)0.24;
(Ⅱ)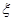 的概率分布列为:
的概率分布列为:
|
|
0 |
2 |
|
P |
0.24 |
0.76 |
其数学期望是: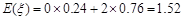
【解析】
试题分析:根据独立事件的概率公式分别求出游客选择游玩甲、乙、丙景点的概率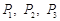 ,分别求出求事件A的概率和
,分别求出求事件A的概率和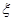 的概率分布列及数学期望.
的概率分布列及数学期望.
试题解析:
解:设该游客选择游玩甲、乙、丙景点的概率依次为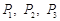 ,由题意知
,由题意知
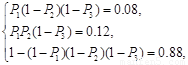 解得
解得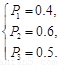 (3分)
(3分)
(Ⅰ)依题意,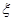 的所有可能取值为0,2.
的所有可能取值为0,2.
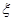 =0的意义是:该游客游玩的旅游景点数为3,没游玩的旅游景点数为0;或游玩的旅游景点数为0,没游玩的旅游景点数为3,
=0的意义是:该游客游玩的旅游景点数为3,没游玩的旅游景点数为0;或游玩的旅游景点数为0,没游玩的旅游景点数为3,
故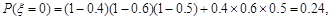 (6分)
(6分)
而函数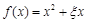 是R上的偶函数时
是R上的偶函数时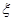 =0,
=0,
所以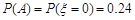 .
(8分)
.
(8分)
(Ⅱ)由(Ⅰ)知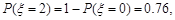 (10分)
(10分)
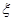 的概率分布列为:
的概率分布列为:
|
|
0 |
2 |
|
P |
0.24 |
0.76 |
其数学期望是: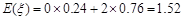 .
(12分)
.
(12分)
考点:独立事件的概率


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲,乙两个旅游团所选旅游线路不同的概率.
(2)某天上午9时至10时, 甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com