
【题目】已知抛物线![]() 的焦点为
的焦点为![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 横坐标为
横坐标为![]() 时,
时,![]() 为正三角形.
为正三角形.
(1)求![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和
和 ![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
①证明直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
②![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①证明见解析,
;(2)①证明见解析,![]() ;②存在,
;②存在,![]() .
.
【解析】
试题分析:(1)根据抛物线的焦半径公式,结合等边三角形的性质,求出![]() 的值,即可求解抛物线的方程;(2)①设出点
的值,即可求解抛物线的方程;(2)①设出点![]() 的坐标,求出直线
的坐标,求出直线![]() 的方程,利用
的方程,利用![]() ,且
,且![]() 和
和![]() 有且只有一个公共点
有且只有一个公共点![]() ,求出点
,求出点![]() 的坐标,写出直线
的坐标,写出直线![]() 的方程,将方程化为点斜式,即可求解定点的坐标;②中由①知直线
的方程,将方程化为点斜式,即可求解定点的坐标;②中由①知直线![]() 过焦点
过焦点![]() ,所以
,所以![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,再由直线的点斜式,利用点到直线的距离公式,再利用基本不等式即可求解结论.
,再由直线的点斜式,利用点到直线的距离公式,再利用基本不等式即可求解结论.
试题解析:(1)由题意知![]() ,设
,设![]() ,则
,则![]() 的中点为
的中点为![]() ,因为
,因为![]() ,由抛物线的定义知
,由抛物线的定义知![]() ,解得
,解得![]() 或
或![]() (舍去).由
(舍去).由![]() ,解得
,解得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() .
.
(2)①证明:由(1)知![]() ,设
,设![]() ,因为
,因为![]() ,则
,则![]() ,由
,由![]() 得,
得,![]() ,故
,故![]() ,故直线
,故直线![]() 的斜率
的斜率![]() ,因为直线
,因为直线![]() 和直线
和直线![]() 平行,设直线
平行,设直线![]() 的方程为
的方程为![]() ,代人抛物线的方程得
,代人抛物线的方程得![]() ,由题意
,由题意![]() ,得
,得![]() ,设
,设![]() ,则
,则![]() ,当
,当![]() 时,
时,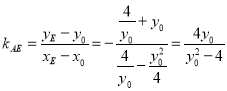 ,可得直线
,可得直线![]() 的方程为
的方程为![]() ,由
,由![]() ,整理可得
,整理可得![]() ,直线
,直线![]() 恒过点
恒过点![]() .当
.当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过点
,过点![]() .所以直线
.所以直线![]() 过定点
过定点![]() .
.
②由①知直线![]() 过焦点
过焦点![]() ,所以
,所以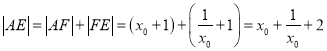 .设直线
.设直线![]() 的方程为
的方程为![]() ,因为点
,因为点![]() 在直线
在直线![]() 上,故
上,故![]() ,设
,设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,由
,由![]() ,得
,得![]() ,代人抛物线的方程得
,代人抛物线的方程得![]() ,所以
,所以![]() ,可求得
,可求得![]() .所以点
.所以点![]() 到直线
到直线![]() 的距离为
的距离为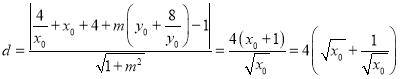 ,则
,则![]() 的面积
的面积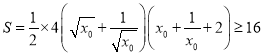 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立.所以
时,等号成立.所以![]() 的面积的最小值为
的面积的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设命题![]() 对任意实数
对任意实数![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线.
轴上的双曲线.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题:“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2009年推出一种新型家用轿车,购买时费用为![]() 万元,每年应交付保险费、养路费及汽油费共
万元,每年应交付保险费、养路费及汽油费共![]() 万元,汽车的维修费为:第一年无维修费用,第二年为
万元,汽车的维修费为:第一年无维修费用,第二年为![]() 万元,从第三年起,每年的维修费均比上一年增加
万元,从第三年起,每年的维修费均比上一年增加![]() 万元.
万元.
(1)设该辆轿车使用![]() 年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为
年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为![]() ,求
,求![]() 的表达式;
的表达式;
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
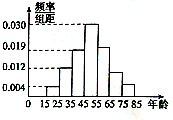
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中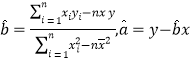 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com