
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为q(q≠1).令A=
为等比数列,公比为q(q≠1).令A=![]() .A={1,2},
.A={1,2},
(1)当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,q>0,试比较
,q>0,试比较![]() 与
与![]() (n≥3)的大小?并证明你的结论.
(n≥3)的大小?并证明你的结论.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】阅读下面一道题目的证明,指出其中的一处错误。题目:平面上有六个点,任何三点都是三边互不相等三角形的顶点,则这些三角形中有一个的最短边又是另一个三角形的最长边。证明:第一步,对已知的六个点作两两连线,可以得出15条边,记为![]() ,
,![]() ,…,
,…,![]() .第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设
.第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设![]() .第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则
.第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则![]() 、
、![]() 、
、![]() 组成的三角形的最长边
组成的三角形的最长边![]() ,也是
,也是![]() 、
、![]() 、
、![]() 组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①若![]() 为真命题,则
为真命题,则![]() 为真命题;
为真命题;
②命题“![]() ,有
,有![]() ”的否定为“
”的否定为“![]() ,有
,有![]() ”;
”;
③“平面向量![]() 与
与![]() 的夹角为钝角”的充分不必要条件是“
的夹角为钝角”的充分不必要条件是“![]() ”;
”;
④在锐角三角形![]() 中,必有
中,必有![]() ;
;
⑤![]() 为等差数列,若
为等差数列,若![]() ,则
,则![]()
其中正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.
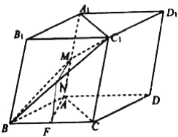
(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() .
.
(1)过曲线![]() 的左顶点作
的左顶点作![]() 的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
的两条渐近线的平行线,求这两组平行线围成的平行四边形的面积;
(2)设斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
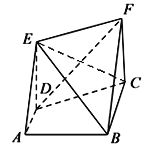
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的正弦值;
所成二面角的正弦值;
(Ⅲ)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com