
【题目】学校计划在全国中学生田径比赛期间,安排6位志愿者到4个比赛场地提供服务,要求甲、乙两个比赛场地各安排一个人,剩下两个比赛场地各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( )
A. 168种 B. 156种 C. 172种 D. 180种
【答案】B
【解析】分析:据题意,用间接法分析,先分4步进行分析不受限制的排法数目,再排除计算其中小李和小王在一起的排法数目,计算即可得答案.
详解:根据题意,设剩下的2个场地为丙和丁,
用间接法分析:
先计算小李和小王不受限制的排法数目:先在6位志愿者中任选1个,安排到甲,有C61=6种情况,再在剩下的5个志愿者中任选1个,安排到乙,有C51=5种情况,
最后将剩下的4个志愿者平均分成2组,全排列后安排到剩下的2个场地,有
![]() 则小李和小王不受限制的排法有6×5×6=180种,
则小李和小王不受限制的排法有6×5×6=180种,
若小李和小王在一起,则两人去丙或丁,有2种情况,
在剩下的4位志愿者中任选1个,安排到甲,有C41=4种情况,
再在剩下的3个志愿者中任选1个,安排到乙,有C31=3种情况,
最后2个安排到剩下的场地,有1种情况,
则小李和小王在一起的排法有2×4×3=24种,
则小李和小王不在一起排法有180-24=156种;
故选B.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数![]()
的分布列及数学期望.
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,若
,若![]() 、
、![]() 、
、![]() 是
是![]() 的三条边长,则下列结论:①对于一切
的三条边长,则下列结论:①对于一切![]() 都有
都有![]() ;②存在
;②存在![]() 使
使![]() 、
、![]() 、
、![]() 不能构成一个三角形的三边长;③
不能构成一个三角形的三边长;③![]() 为钝角三角形,存在
为钝角三角形,存在![]() ,使
,使![]() ,其中正确的个数为______个
,其中正确的个数为______个
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1 , A1D1的中点,点P,Q分别在棱DD1 , BB1上移动,且DP=BQ=λ(0<λ<2) 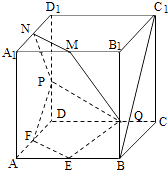
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={(x1 , x2 , x3 , x4 , x5)|xi∈{﹣1,0,1},i={1,2,3,4,5},那么集合A中满足条件“1≤|x1|+|x2|+|x3|+|x4|+|x5|≤3”的元素个数为( )
A.60
B.90
C.120
D.130
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图. 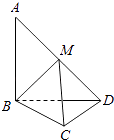
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com