
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() (其中
(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 如图所示.
如图所示.
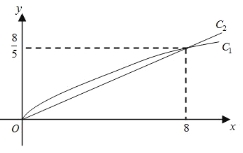
(1)求函数![]() 的解析式;
的解析式;
(2)若该商场一共投资8万元经销甲、乙两种商品,求该商场所获利润的最大值.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.

(1)求证:BC∥DE;
(2)若D、E、C、F四点共圆,且![]() ,求∠BAC.
,求∠BAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点![]() 为中心的
为中心的![]() 海里以内海域被设为警戒水域.点
海里以内海域被设为警戒水域.点![]() 正北
正北![]() 海里有一个雷达观测站
海里有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过
,经过![]() 分钟又测得该船已行驶到点
分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() (其中
(其中![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
,![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在区间
定义在区间![]() 内,对于任意的
内,对于任意的![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() .
.
(1)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(2)判断这样的函数是否具有奇偶性和单调性,并加以证明;
(3)若![]() ,求方程
,求方程![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中开展了丰富多彩的社团文化活动,甲,乙,丙三位同学在被问到是否参加过街舞社,动漫社,器乐社这三个社团时,
甲说:我参加过的社团比乙多,但没有参加过动漫社;
乙说:我没有参加过器乐社;
丙说:我们三个人都参加过同一个社团,由此判断乙参加过的社团为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
计算得K2=10,则下列选项正确的是( )
A. 有99.5%的把握认为使用智能手机对学习有影响
B. 有99.5%的把握认为使用智能手机对学习无影响
C. 在犯错误的概率不超过0.1%的前提下,认为使用智能手机对学习有影响
D. 在犯错误的概率不超过1%的前提下,认为使用智能手机对学习无影响
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com