已知等比数列{an}满足:a3+a4+a5=28,且a4+2是a3、a5的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}单调递减,其前n项和为Sn,求使Sn>127成立的正整数n的最小值.
【答案】
分析:(Ⅰ)设等比数列{a
n}的公比为q,首项为a
1依题意有2(a
4+2)=a
3+a
5,a
3+a
4+a
5=28,且a
4+2是a
3、a
5的等差中项.由此能够推导出a
n.
(Ⅱ)求出S
n由题意可得 S
n>127,由此能求出满足条件的n的最小值.
解答:解:(I)设等比数列{a
n}的首项为a
1,公比为q,
依题意,有2(a
4+2)=a
3+a
5,
代入a
3+a
4+a
5=28,,得a
4=8
∴a
3+a
5=20,. …(2分)
∴
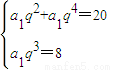
解之得

或

…(6分)
∴a
n=2
n-1或a
n=2
7-n. …(8分)
(II)又{a
n}单调递减,∴
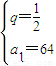
. …(9分)
则
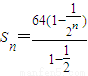
=
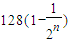
. …(10分)
∴

,即
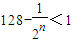
,∴2
n>128,
∴n>7.
故使S
n>128成立的正整数n的最小值为8.…(12分)
点评:本题考查数列的性质和综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,灵活地运用公式解答.

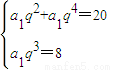 解之得
解之得 或
或 …(6分)
…(6分)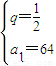 . …(9分)
. …(9分)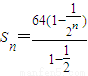 =
=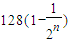 . …(10分)
. …(10分) ,即
,即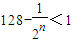 ,∴2n>128,
,∴2n>128,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案