
【题目】设集合A中含有三个元素3,x,x2﹣2x.
(1)求实数x应满足的条件;
(2)若﹣2∈A,求实数x.
科目:高中数学 来源: 题型:
【题目】某校选择高一年级三个班进行为期二年的教学改革试验,为此需要为这三个班各购买某种设备1台.经市场调研,该种设备有甲乙两型产品,甲型价格是3000元/台,乙型价格是2000元/台,这两型产品使用寿命都至少是一年,甲型产品使用寿命低于2年的概率是![]() ,乙型产品使用寿命低于2年的概率是
,乙型产品使用寿命低于2年的概率是![]() .若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
.若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
(1)若该校购买甲型2台,乙型1台,求试验期内购买该种设备总费用恰好是10000元的概率;
(2)该校有购买该种设备的两种方案, ![]() 方案:购买甲型3台;
方案:购买甲型3台; ![]() 方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2|x﹣a|(a∈R).
(1)若函数f(x)为偶函数,求a的值;
(2)当a>0时,若对任意的x∈[0,+∞),不等式f(x﹣1)≤2f(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
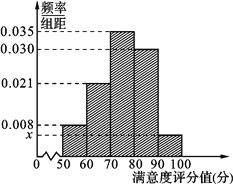
(Ⅰ) 求图中![]() 的值;
的值;
(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取2人进行座谈,求所抽取的两人中至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,下列四组函数中表示相等函数的是( )
A.y=logax与y=(logxa)﹣1
B.y=2x与y=logaa2x
C.![]() 与y=x
与y=x
D.y=logax2与y=2logax
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果集合A,B,同时满足A∪B={1,2,3,4},A∩B={1},A≠{1},B≠{1},就称有序集对(A,B)为“好集对”.这里有序集对(A,B)意指,当A≠B时,(A,B)和(B,A)是不同的集对,那么“好集对”一共有( )个.
A.5
B.6
C.7
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com