
 所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.
所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标. (θ为参数 )试判断他们的公共点个数;
(θ为参数 )试判断他们的公共点个数; ,x大于等于0小于
,x大于等于0小于 和x小于0,分别化简绝对值后,求出解集,即可得到原不等式的解集.三个题中任选两个作答即可.
和x小于0,分别化简绝对值后,求出解集,即可得到原不等式的解集.三个题中任选两个作答即可. (x,y)=(13,5),即
(x,y)=(13,5),即 ,
,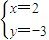 ,所以A(2,-3);
,所以A(2,-3); ,则
,则 •
• =
= ,即
,即 ,
, ,解得a=-1,b=3,c=-1,d=2
,解得a=-1,b=3,c=-1,d=2 ;
; =
= <2=r,得到直线与圆的位置关系是相交,
<2=r,得到直线与圆的位置关系是相交, 时,原不等式变为:2x-1<x+1,解得x<2,所以原不等式的解集为[
时,原不等式变为:2x-1<x+1,解得x<2,所以原不等式的解集为[ ,2);
,2); 时,原不等式变为:1-2x<x+1,解得x>0,所以原不等式的解集为[0,
时,原不等式变为:1-2x<x+1,解得x>0,所以原不等式的解集为[0, );
);

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
|
|
|
|
| 5 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题十七 选修系列 题型:解答题
本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题作答,满分14分。如果多做,则按所做的前两题记分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵M= ,N=
,N= ,且MN=
,且MN= 。
。
(Ⅰ)求实数a,b,c,d的值;(Ⅱ)求直线y=3x在矩阵M所对应的线性变换作用下的像的方程。
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线L的参数方程为 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 =2
=2 sin
sin 。
。
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线L交于点A,B。若点P的坐标为(3, ),求∣PA∣+∣PB∣。
),求∣PA∣+∣PB∣。
(3)(本小题满分7分)选修4-5:不等式选讲
已知函数f(x)= ∣x-a∣.
(Ⅰ)若不等式f(x)  3的解集为
3的解集为 ,求实数a的值;
,求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源:福建 题型:解答题
|
|
|
|
| 5 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2010年福建省高考数学试卷(理科)(解析版) 题型:解答题
 ,
, ,且
,且 ,
, (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ,
,查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:新课标4系列选考内容(解析版) 题型:解答题
 ,
, ,且
,且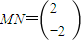 ,
,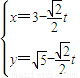 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com